太阳能光伏技术中的最大功率点跟踪

一般在正常工作情况下，随光强和温度变化的光伏电池U－I和P－U特性曲线分别如图10．41、图10．42所示。显然，光伏电池运行受外界环境温度、光强等因素的影响，呈现出典型的非线性特征。一般来说，理论上很难得出非常精确地光伏电池数学模型，因此通过数学模型的实时计算来对光伏系统进行准确的MPPT控制是困难的。

图10．41　相同温度而不同光强条件下光伏电池特性　（a）U－I特性　（b）P－U特性　

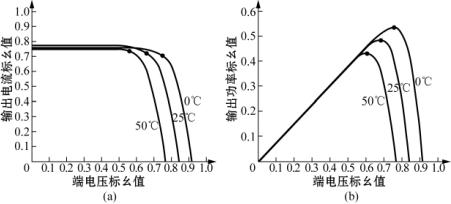
图10．42　相同光强而不同温度条件下光伏电池特性（a）U－I特性　（b）P－U特性

理论上，根据电路原理：当光伏电池的输出阻抗和负载阻抗相等时，光伏电池的输出功率最大，可见，光伏电池的MPPT过程实际上就是基于光伏电池输出阻抗和负载阻抗等值相匹配的过程。由于光伏电池的输出阻抗受环境因素的影响，因此，如果能通过控制方法实现对负载阻抗的实时调节，并使其跟踪光伏电池的输出阻抗，就可以实现光伏电池的MPPT控制。为了方便讨论，光伏电池的等效阻抗Ropt被定义成最大功率点电压Umpp和最大功率点电流Impp的比值，即Ropt＝Umpp／Impp。显然，当外界环境发生变化时，Ropt也将发生变化。但是，由于实际应用中的光伏电池是向一个特定的负载传输功率，因此就存在一个负载匹配的问题。

光伏电池的伏安特性与负载特性及其匹配的过程如图10．43所示，图中光伏电池的负载特性以一过坐标原点的电阻特性表示。由图10．43可以看出：在光强1的情况下，电路的实际工作点正好处于负载特性与光伏U－I特性曲线的交点a处，而a点正好是光伏电池的最大功率点（MPP），此时光伏电池的伏安特性与负载阻特性相匹配；但在光强2的情况下，电路的实际工作点则处于b处，而此时的最大功率点却在a′处，为此，必须进行相应的负载阻抗的匹配控制，而使电路的实际工作点处于最大功率点a′处，从而实现光伏电池的最大功率发电。

图10．43　光伏电池的伏安特性与负载特性的匹配

传统的MPPT方法依据判断方法和准则的不同被分为开环和闭环MPPT方法。

实际上，外界温度、光照和负载的变化对光伏电池输出特性曲线的影响呈现出一些基本的规律，比如光伏电池的最大功率点电压Umpp与光伏电池的开路电压Uoc之间存在近似的线性关系等。基于这些规律，可提出一些开环的MPPT控制方法。本章10．8．1．1节简要介绍了基于输出特性曲线的开环MPPT方法，这一类方法简便易行，减少了工作点在远离最大功率点区域的MPPT时间，但对光伏电池的输出特性有较强的依赖性，只是近似跟踪最大功率点，效率较低，实际中常常和直接跟踪方法配合使用。

闭环MPPT方法则通过对光伏电池输出电压和电流值的实时测量与闭环控制来实现MPPT，使用的最广泛的自寻优类算法即属于这一类。典型的自寻优类MPPT算法有扰动观测法和电导增量法，这两种MPPT方法将在本章10．8．1．2节和10．8．1．3节中简单介绍。

10．8．1．1 基于输出特性曲线的开环MPPT方法

基于输出特性曲线的开环MPPT方法是从光伏电池的输出特性曲线的基本规律出发，通过简单的开环控制来实现MPPT。

由图10．41可以看出：当温度相同时，随着光强的增加，光伏电池的开路电压几乎不变，而短路电流、最大输出功率则有所增加，可见光强度变化时主要影响光伏电池的输出电流；另外，由图10．42可以看出：当光强相同时，随着温度的增加，光伏电池的短路电流几乎不变，而开路电压、最大输出功率则有所减小，可见温度变化时主要影响光伏电池的输出电压。针对上述基本规律，可以提出几种基于光伏电池输出特性曲线的开环MPPT方法，简要介绍如下。

1）定电压跟踪法

由图10．41可知，在光强大于一定值并且温度变化不大时，光伏电池的输出P－U曲线上的最大功率点几乎分布于一条垂直直线的两侧附近。因此，若能将光伏电池输出电压控制在其最大功率点附近上的某一定电压处，光伏电池将获得近似的最大功率输出，这种MPPT控制称为定电压跟踪法。

进一步研究发现，光伏电池的最大功率点电压Umpp与光伏电池的开路电压Uoc之间存在近似的线性关系，即

式中：系数k1的值取决于光伏电池的特性，一般k1的取值大约在0．8左右。

定电压跟踪法实际上是一种开环的MPPT算法，其控制简单快速，但由于忽略了温度对光伏电池输出电压的影响，因此，温差越大，定电压跟踪法跟踪最大功率点的误差也就越大。

虽然定电压跟踪法难以准确实现MPPT，但其具有控制简单并快速接近最大功率点的优点，因此电压跟踪法常与其他闭环MPPT方法组合使用，即一般可以在光伏系统启动过程中先采用定电压跟踪法使工作点电压快速接近最大功率点电压，然后再采用其他闭环的MPPT算法进一步搜索最大功率点。这种组合的MPPT方法可以有效降低启动过程中对远离最大功率点区域进行搜索所造成的功率损耗。

另外，电压跟踪法一般可以用于低价且控制要求不高的简易系统中。

2）短路电流比例系数法

由图10．41可知，在光强大于一定值并且温度变化不大时，光伏电池的输出U－I曲线最大功率点电流Impp与光伏电池短路电流Isc也存在近似的线性关系，即

式中：系数k2的值取决于光伏电池的特性，一般k2的取值大约在0．8左右。

实际应用时，可以在逆变器中添加相关的功率开关，并通过周期性短路光伏电池的输出端来测得Isc。该方法与定电压跟踪法的应用类似，实际上也属于开环的MPPT算法。

定电压跟踪法和短路电流比例系数法的主要优点就是控制简单且易于实现。但由于式（10－17）和式（10－18）是近似的公式，所以光伏电池并不是工作在真正的最大功率点上，常常需要和其他的MPPT算法配合使用，以获取较好的快速性和精确性。

同时由于测量Uoc要将负载侧断开，所以存在瞬时的功率损失，而测量Isc比测量Uoc更加复杂，因此短路电流比例系数法实际中较少应用。10．8．1．2 扰动观测法（P ＆O法）

扰动观测法（perturbation and observation method，P ＆O）是实现MPPT最常用的自寻优类方法之一。其基本思想是：首先扰动光伏电池的输出电压（或电流），然后观测光伏电池输出功率的变化，根据功率变化的趋势连续改变扰动电压（或电流）方向，使光伏电池最终工作于最大功率点。对于并网光伏系统而言，从观测对象来说，扰动观测法又可以分为两种，一种是基于并网逆变器输入参数的扰动观测法，另外一种是基于并网逆变器输出参数的扰动观测法。

基于并网逆变器输入参数的扰动观测法直接检测逆变器输入侧光伏电池的输出电压和电流，通过计算光伏电池的输出功率并采用功率扰动寻优的方法来跟踪光伏电池的最大输出功率点；而基于输出参数的扰动观测法则是在不考虑逆变器损耗的情况下，根据功率守恒原理（逆变器输入功率等于逆变器输出功率），通过并网逆变器网侧输出功率扰动寻优的方法来跟踪光伏电池的最大输出功率点，实际上这是一种并网光伏逆变系统的MPPT方法。

以下以基于并网逆变器输入参数的扰动观测法为例介绍其基本原理。

众所周知，一般正常条件下，光伏电池P－U曲线是一个以最大功率点为极值的单峰值函数，这一特点为采用扰动观测法来寻找最大功率点提供了条件，而扰动观测法实际上采用了步进搜索的思路，即：从起始状态开始，每次对输入信号做一有限变化，然后测量由于输入信号变化引起输出变化的大小及方向，待方向辨别后，再控制被控对象的输入按需要的方向调节，从而实现自寻最优控制。将步进搜索应用于光伏系统的MPPT控制时，就是所称的扰动观测法。如图10．43所示：当负载特性与光伏电池特性的交点在最大功率点左侧时，MPPT控制会使交点处的电压升高；而当交点在最大功率点右侧时，MPPT控制会使交点处的电压下降，如果持续这样的搜索过程，最终可使系统跟踪光伏电池的最大功率点运行。

为讨论方便，假定光强、温度等环境条件不变，并设：U，I为上一次光伏电池的电压、电流检测值，P为对应的输出功率，U1，I1为当前光伏电池的电压、电流检测值，P1为对应的输出功率，ΔU为电压调整步长，ΔP＝P1－P为电压调整前后的输出功率差。图10．44显示了扰动观测法的MPPT过程，具体描述如下：(www.xing528.com)

（1）当增大参考电压U（U1＝U＋ΔU）时，若P1＞P，表明当前工作点位于最大功率点的左侧，此时系统应保持增大参考电压的扰动方式，即U2＝U1＋ΔU，其中U2为第二次调整后的电压值，如图10．44（a）所示；

（2）当增大参考电压U（U1＝U＋ΔU）时，若P1＜P时，表明当前工作点位于最大功率点的右侧，此时系统应采用减小参考电压的扰动方式，即U2＝U1－ΔU，如图10．44（b）所示；

（3）当减小参考电压U（U1＝U－ΔU）时，若P1＞P时，表明工作点位于最大功率点的右侧，系统应保持减小参考电压的扰动方式，即U2＝U1－ΔU，如图10．44（c）所示；

（4）当减小参考电压U（U1＝U－ΔU）时，若P1＜P时，表明工作点位于最大功率点的左侧，此时系统应采用增大参考电压的扰动方式，即U2＝U1＋ΔU，如图10．44 （d）所示。

图10．44　扰动观测法MPPT过程示意

（a）增大电压后需继续采用增大电压扰动的过程 （b）增大电压后需采用减小电压扰动的过程（c）减小电压后需继续采用减小电压扰动的过程 （d）减小电压后需采用增大电压扰动的过程

可见，扰动观测法就是按照以上图10．44所示的过程反复进行输出电压扰动，并使其电压的变化不断使光伏电池输出功率向大的方向改变，直到工作点接近最大功率点。扰动观测法按每次扰动的电压变化量是否固定，可以分为定步长扰动观测法和变步长扰动观测法两类，定步长扰动观测法的流程图如图10．45所示。

图10．45　定步长扰动观测法的流程图

以上分析可知，扰动观测法具有控制概念清晰、简单、被测参数少等优点，因此被普遍地应用于实际光伏系统的MPPT控制。值得注意的是，在扰动观测法中，电压初始值及扰动电压步长对跟踪精度和速度有较大影响。

10．8．1．3 电导增量法

最大功率点跟踪实质上是搜索满足条件dP／dU＝0的工作点，由于数字控制中检测及控制精度的限制，常以ΔP／ΔU近似代替dP／dU，从而影响了MPPT算法的精确性。一般而言，ΔU由步长决定，当最小步长一定时，MPPT算法的精度就由ΔP对dP的近似程度决定。扰动观测法用两点功率差近似替代微分dP，即从dP≈Pk－Pk－1出发，推演出以功率增量为搜索判据的MPPT算法。

实际上，为了进一步提高MPPT算法对最大功率点的跟踪精度，可以考虑采用功率全微分近似替代dP的MPPT算法，即从dP＝UdI＋IdU出发，推演出以电导和电导变化率之间的关系为搜索判据的MPPT算法，即电导增量法，以下详细介绍这种MPPT算法。

电导增量法（INC—incremental conductance）从光伏电池输出功率随输出电压变化率规律出发，推导出系统工作点位于最大功率点时的电导和电导变化率之间的关系，进而提出相应的MPPT算法。

图10．46给出了光伏电池P－U特性曲线及dP／dU变化特征，即在光强一定的情况下仅存在一个最大功率点，且在最大功率点两边dP／dU符号相异，而在最大功率点处dP／dU＝0。

显然，通过对dP／dU的定量分析，可以得到相应的最大功率点判据。考虑光伏电池的瞬时输出功率为

图10．46　光伏电池P－U特性的dP／dU变化特征

将式（10－19）两边对光伏电池的输出电压U求导，则

当dP／dU＝0时，光伏电池的输出功率达到最大。则可以推导出工作点位于最大功率点时需满足以下关系：

实际中以ΔI／ΔU近似代替dI／dU，则使用电导增量法（INC）进行最大功率点跟踪时判据如下：

图10．47为定步长电导增量法流程图。其中ΔU＊为每次系统调整工作点时固定的电压改变量（步长）。从图中可以看出计算出ΔU之后，对其是否为零进行判定，使流程图出现两条分支，其中：左分支与上述分析相吻合；而右分支则主要是为抑制当外部光强发生突变时的误判而设置的。

从本质上说，电导增量法和扰动观测法都是求出工作点电压变化前后的功率差，找出满足ΔP／ΔU＝0的工作点，两者的主要区别在于功率差的计算方式。

扰动观测法将dP用功率差ΔP＝Pk－Pk－1进行近似；而电导增量法则是将dP用全微分ΔP＝UΔI＋IΔU进行近似，其中ΔU＝Uk－Uk－1，ΔI＝Ik－Ik－1。

在最大功率点跟踪过程中，电导增量法是在dP／dU＝0（或者dP／dU＝－I／U）时，方能使光伏电池输出最大功率。然而，由于采用与控制精度的限制，实际应用中可以将dP／dU＝0条件改造为dP／dU＜ε，其中ε是在满足最大功率跟踪一定精度范围内的阀值，由具体的要求决定。

图10．47　电导增量法流程图

采用电导增量法的主要优点是MPPT的控制稳定度高，当外部环境参数变化时，系统能平稳地追踪其变化，且与光伏电池的特性及参数无关。然而，电导增量法对控制系统要求则相对较高，另外，电压初始化参数对系统启动过程中的跟踪性能有较大影响，若设置不当则可能产生较大的功率损失。