太阳能光伏技术与应用：并网逆变器控制策略

10．3．3．1 并网逆变器控制策略简介

光伏并网逆变器的控制策略是光伏系统并网控制的关键。并网逆变器有两个基本控制要求，即：一是要保持前后级之间的直流侧电压稳定；二是要实现并网电流控制（网侧单位功率因数正弦波电流控制），甚至需根据指令进行电网的无功调节。网侧逆变器是光伏并网发电系统的核心，下面简单介绍其控制策略。

间接电流控制通过控制并网逆变器交流侧电压矢量来间接控制输出电流矢量。其无需电流检测且控制简单，但也存在明显不足：①对系统参数变化较为敏感；②由于其基于系统的稳态模型进行控制因而动态响应速度慢；③由于无电流反馈控制，因而并网逆变器输出电流的波形品质难以保证，甚至在动态过程中含有一定的直流分量。

直接电流控制可以克服间接电流控制方案的上述不足，其依据系统动态数学模型，构造了电流闭环控制系统，不仅提高了系统的动态响应速度和输出电流的波形品质，同时也降低了其对参数变化的敏感程度，提高了系统的鲁棒性。

在直接电流控制前提下，如果以电网电压矢量进行定向（VOC），通过控制并网逆变器输出电流矢量的幅值和相位（相对于电网电压矢量），即可控制并网逆变器的有功和无功功率，以此实现逆变器的并网控制。

VOC是在电压定向基础上通过输出电流矢量的控制实现对并网逆变器输出有功和无功功率的控制。实际上，如果在电压定向基础上，不对输出电流进行控制，而是对并网逆变器的有功和无功功率进行直接控制，也可以实现逆变器的并网控制。这种在电压定向基础上的并网逆变器的直接功率控制（DPC）一般称为基于电压定向的直接功率控制（V－DPC）。

上述VOC和V－DPC两种并网逆变器控制策略的控制性能均依赖于电网电压矢量位置的准确获得，获得电网电压矢量位置的一般方法是：首先检测电网电压瞬时值ea，eb，ec，再由三相静止坐标系（abc）到两相静止坐标系（αβ）的坐标变换获得其在αβ坐标系下的表达式eα，eβ，从而获得电压矢量的位置角γ，即

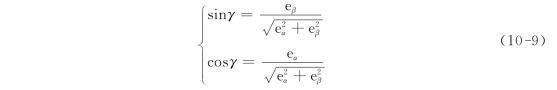
上述电压定向方法的不足在于：由于实际的电网电压并是非理想的正弦波电压，即电网电压除基波分量外还含有丰富的谐波分量，因此使得电网电压的检测值中除基波成分外还包含谐波成分，这样就使得基波电压定向出现偏差，从而降低了系统有功、无功的控制性能。

解决以上不足的方法有两种：一种可行的解决方法是加入基于电网电压基波的锁相环（PLL）技术，以期实现对电网电压基波量进行定向，但这需要对锁相环进行动态响应与稳态精度的折中设计，定向好坏取决于锁相环的设计性能；另一种简单的解决方法是采用虚拟磁链进行定向，由于虚拟磁链实际上是电网电压的积分，而积分的低通特性则对电网电压中的谐波分量有一定的抑制作用，从而有效克服了电网电压谐波对矢量定向精度的影响。

总之，根据矢量定向和控制变量的不同，并网逆变器的控制策略可以归类成如下四类，即：①基于电压定向的矢量控制（VOC）；②基于电压定向的直接功率控制（V－DPC）；③基于虚拟磁链定向的矢量控制（VFOC）；④基于虚拟磁链定向的直接功率控制（VF－DPC）。相应的控制策略的组合关系如图10．19所示。

图10．19　并网逆变器控制策略的分类关系

10．3．3．2 三相并网逆变器的控制策略

下面介绍一种常见的基于电压矢量定向的双闭环控制［6］。其控制结构如图10．20所示。

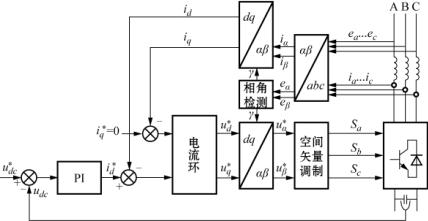
图10．20　基于电压矢量定向的控制系统（VOC）示意图

图中三相电网电压测量值；γ为电网电压矢量的位置角；udc为直流电压的测量值；Sa，Sb， Sc为逆变器a，b，c三相的开关函数。

基于电压矢量定向的双闭环控制三相并网逆变器控制系统由电压外环和电流内环构成，其控制原理如下：

1）电压外环

控制系统由直流电压外环和有功、无功电流内环组成。直流电压外环的作用是为了稳定或调节直流电压，显然，引入直流侧电压反馈并通过一个PI调节器即可实现直流电压的无静差控制。由于直流电压的控制可通过id的控制来实现，因此直流电压外环PI调节器的输出量即为有功电流内环的电流参考值，从而对并网逆变器输出的有功功率进行调节。无功电流内环的电流参考值则是根据需向电网

输送的无功功率参考值q＊且由q＊＝运算而得，当令

＝0时，并网逆变器运行于单位功率因数状态，即仅向电网输送有功功率。

2）电流内环(www.xing528.com)

电流内环是在dq坐标系中实现控制的，即：并网逆变器输出电流的检测值ia，ib，ic经过abc／αβ／dq的坐标变换转换为同步旋转dq坐标系下的直流量id，iq，将其与电流内环的电流参考值进行比较，并通过相应的PI调节器控制分别实现对id，iq的无静差控制。电流内环PI调节器的输出信号经过dq／αβ逆变换后，即可通过空间矢量调制（SVPWM）得到并网逆变器相应的开关驱动信号Sa，Sb，Sc，从而实现逆变器的并网控制。另外，图10．20中的坐标变换的相角信息γ是通过式（10－9）计算得到得，其中的eα，eβ值是通过检测电网电压（ea，eb，ec）并经abc／αβ的坐标变换运算得到的。

在三相静止abc坐标系下，并网逆变器的电压方程为：

式中：矢量Xabc＝（xa，xb，xc）T，x表示相应的物理量，下标表示abc坐标系中各相的变量。

当只考虑三相平衡系统时，系统只有两个自由度，即三相系统可以简化成两相系统，因此可将三相静止abc坐标系下的数学模型变换成两相垂直静止αβ坐标系下的模型，即

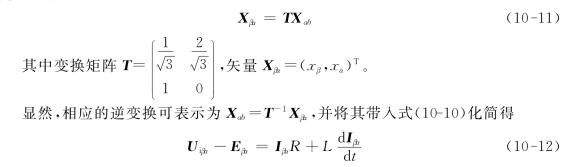
再将两相静止αβ坐标系下的数学模型变换成同步旋转dq坐标系下的数学模型，即：

式中：ω0为同步旋转角频率，且ω0＝dθ／dt。

在零初始状态下，对式（10－14）进行拉氏变换，可得到系统在同步旋转dq坐标系下并网逆变器频域的数学模型为：

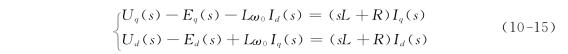
与式（10－15）相对应的模型结构，如图10．21所示。

图10．21　系统在同步坐标系下的模型

图10．22　引入前馈解耦的模型结构

显然，从图10．21可以看出：在dq坐标系中，并网逆变器的数学模型在d，q轴间存在耦合，为了实现dq轴的解耦控制，通常可以采用较为简单的前馈解耦策略，如图10．22所示，即在并网逆变器输出交流电压中分别引入前馈量＋Lω0Id（s）和－Lω0Iq（s），使其与图10．22模型中的耦合项－Lω0Id（s）和＋Lω0Iq（s）分别进行对消，从而实现了dq轴间的解耦，解耦后的系统模型转化为相互独立且完全对等的两部分。前馈解耦实际上是一种开环解耦方案，其控制简单且不影响系统稳定性，然而这种前馈解耦的性能依赖于系统参数，因而难以实现完全的解耦，因此实际上前馈解耦是一种削弱耦合的补偿控制。

10．3．3．3 单相并网逆变器的控制策略

在中小功率单相并网逆变器中，其输出LCL滤波器的电容一般较小，因此可以考虑采用较为简单的双环控制策略，其系统及控制结构如图10．23所示。

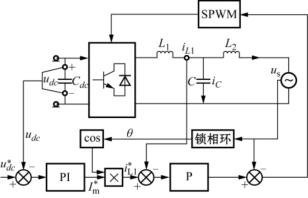
图10．23　基于PI，P调节器的单相并网逆变器的双环控制系统结构

图10．23中：并网逆变器的直流电压外环采用PI调节器，通过稳定直流侧电压实现逆变器输入、输出能量的平衡；电流内环的电流幅值参考值由直流电压外环调节器的输出给定，通过检测获得电网电压相位角θ，并由cosθ，的乘积获得瞬时输出电流的参考信号，电流内环一般可采用简单的P调节器，以实现电流的快速控制；为了抑制电网电压扰动，采用了电网电压前馈控制，电流环的输出与电网电压的前馈信号迭加后经过SPWM调制后输出驱动开关管，以实现单相逆变器的并网控制。