表4．1中所列栅线遮蔽因素、栅线及其接触电阻因素及载流子复合因素三者相互关联，还涉及电池正面掺杂浓度与深度的优化选择，从加深理论认识和加强技术掌握角度都十分值得对它们作进一步分析介绍。
栅线包括细栅线和主栅线，后者只有两条或三条，其宽度由组件连接封装要求决定，这里只讨论细栅线宽度与密度的选择。栅线遮蔽程度，或栅线粗细与疏密程度的选择，显然是一个与栅线相关串联内阻大小相互平衡优化的问题，还需考虑栅线间空隙表层中电流向栅线横向输送中的功率损失，分列如下：
栅线遮蔽所致效率相对损失：
式中：a，b分别为栅线宽度、间距；Rcc＝Voc／Isc；ρs为电池表层方块电阻；Jm，Vm为电
为一常数，其中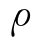
为栅线材料电阻
率，ρc为栅线与电池表面接触电阻率，l为计量栅线电阻时的有效栅线长度，h为栅线平均高度，A为电池面积。
最终的选择应使（1－Δrs）（1－ΔrR）（1－Δrig）≈1－（Δrs＋ΔrR＋Δrig）最大，或使（Δrs＋ΔrR＋Δrig）最小。对a、b的优选结果将与式中电池表层方块电阻（sheet resistance）ρs有关，而它则由表面掺杂浓度ND（假定衬底为P型）和深度d（p－n结深度）决定：显然高掺和深掺是有利于减小方阻ρs的；此外高掺还将改善表层与栅线的欧姆接触，从而减小ρc。仅从以上问题考虑，掺杂浓度和深度应该尽可能大（高掺和深结），使得表面横向电流欧姆损失尽可能小。但高掺和深结又都有其另一面不利因素，分述如下。(www.xing528.com)
高掺将会使得载流子复合率提高，过高的掺杂（＞1020／cm3）甚至使表面出现“死层”，即在此层内光激发产生的载流子立刻被复合，完全没有机会被p－n结收集。因此表层掺杂浓度ND应存在一个最佳值。在4．4节中我们曾计算两种P型硅太阳电池转换效率随表层掺杂浓度ND变化情况，结果如图4．11所示。它们都显示这个最佳值的存在。该计算中实际还未考虑掺杂浓度对接触电阻的影响，如考虑进来这个影响，最佳值还应稍向右移。
深结的不利因素与入射光的吸收衰减分布及光激发非平衡载流子被p－n结所收集的几率分布有关，示意如图4．15所示。这样的分布组合使表层激发的大量载流子不能被p－n结收集而损失。所以在工艺许可的条件下，应尽可能地使p－n结向表面靠近，这是20世纪80年代就已由理论和实践确立的原则，迄今没有改变。图4．16示出对扩散渐变结与均匀突变结电池效率随结深变化的PC1D计算分析结果。可以看到如无工艺问题，浅结的优势可一直持续到十纳米量级；同时结合图4．11还可推测，离子注入的优势可能其实并不在其p－n结为突变型，而在于其深度控制能力，能够获得更浅的结。
图4．15 硅晶体太阳电池表面附近光吸收与光生载流子收集几率分布示意图
全面的优化应该是将掺杂浓度与结深的影响定量描述后与前述三项［式（4－22）～式（4－24）］一并作系统优化。但实践中在结深上尚有工艺限制，不是想要多浅就可多浅，因此实践中优化问题变得更简单了：优先尽量做浅结，而后选择最优掺杂浓度，这样就确定了电池方阻ρs，针对这个值再就前述三项进行优化。
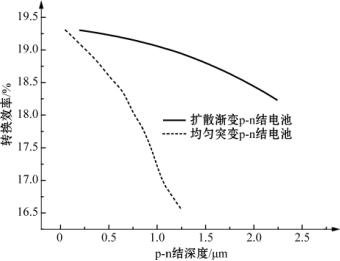
图4．16 均匀突变p－n结与扩散渐变p－n结p型硅太阳电池转换效率随p－n结深度的变化（PC1D计算结果，其他电池与辐照条件与图4．11所示的相同，两类电池掺杂浓度各选图4．11所得峰值浓度）
免责声明：以上内容源自网络，版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。
