太阳电池效率的自然局限及其应用

依靠半导体p－n结的太阳电池将太阳光能量转换为电能的效率受到几项自然因素的局限。最突出的两项相互关联：一是太阳光有其固有光谱；二是半导体材料有其固有禁带宽度。这两大因素使得太阳光中波长大于吸收限λ0（见3．6节）的部分对光伏发电完全无效；而太阳光中波长小于吸收限的部分，即使其每个光子都激发产生一对载流子，其光子能量大于禁带宽度的部分，一般通过热振动释放，或者说转变为热，也是全部多余无效的。剩余有效部分的能量占总的太阳光入射能量的比例，ηs－g，可以针对具体半导体吸收限λ0（对应禁带宽度Eg）和入射光谱P（λ）进行计算，依前述含义有

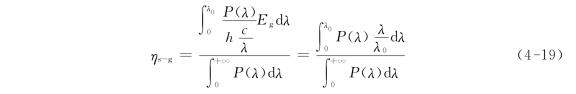
式中：c为光速，hc／λ为光子能量，P（λ）／（hc／λ）即为太阳光中波长为λ的光子的流量密度。

图4．13为标准地面太阳光（AM1．5）垂直照射谱［10］，和计算得出的入射光谱中对晶体硅太阳电池（λ0＝1 107nm）的有效部分的范围（图中阴影部分），其面积为该有效部分的能量，即为式（4－19）的分子，该式分母即为标准光谱下的总面积，计算得到ηs－g＝49%。

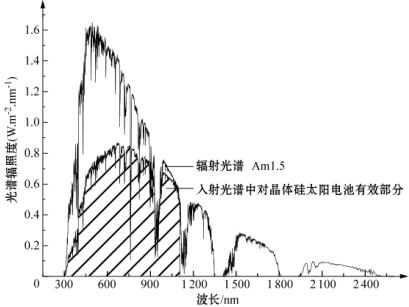
图4．13　标准太阳光谱（AM1．5）及其对吸收限为λ0的半导体同质p－n结太阳电池的无效部分

但是这部分有效光能还是未能全部转变为输出电能。光激发时，每个光子给每个光生电子提供了有效能量Eg，使之跨越了禁带，然而电池输出光生电流时的电压却明显低于禁带的电势差Eg／q。对硅晶体太阳电池而言，禁带电势差为1．12V，而电池开路电压在最理想情况下亦只能达到0．75V，按上限水平估计最大输出功率点电压，Vm＝90%Voc，＝0．675V。这部分能效为0．675／1．12＝60%。这样一来，从入射太阳光起计的能量效率就降到了60%ηs－g，约为29．4%。(www.xing528.com)

第三项自然局限可称为p－n结暗电流损失，它来自电池p－n结本身，无论其材料和工艺质量如何理想，它都不免面临这样一个境况：它在光照下产生的输出电压同时成为加在它自身的正偏压——再看一下理想太阳电池等效电路［见图4．4（a）］就清楚了。它导致一个与光生电流方向相反的净扩散电流。正偏压抵消一部分内建电势，打破了原有漂移与扩散的平衡，故有此净扩散电流Ii。其大小可由肖克莱方程近似给出，为p－n结二极管暗电流。它给效率带来的相对损失应为Iim／Iph＝Iim／Isc，下标m代表最大输出效率点。对理想电池，其值可按输出功率极值条件求解，但得不到表达式，需输入具体数值如饱和电流与光生电流之比I0／Iph等计算作图求解，对硅晶太阳电池得到上述相对损失为6%～10%。取其下限6%，则效率上限降低为94%×29．4%，取为27．6%。

第四项自然局限来自温度，太阳电池作为一种半导体器件，温度总是其性能的自然限制因数。理论和经验都表明太阳电池效率随温度线性变化，理论推得晶硅太阳电池绝对值随温度变化的比例系数约为－0．04%／℃。因此我们需时刻清楚太阳电池的转换效率受到温度的自然局限。注意，由于上述估算中对电池输出电压等参数的估计值为常温下的经验值，其中已包含温度影响，所以不能把所得效率极限27．6%当做0K时的理想效率。

用PC1D计算，输入完全理想条件（无反射、无漏电、无串联内阻、无杂质缺陷复合中心、无表面复合），得到地面标准太阳光（AM1．5）照射条件下，温度为25／℃时，晶体硅电池理想条件下效率为26．8%，开路电压为0．75V。与以上估计颇为接近。

马丁·格林［1］对自然局限下硅太阳电池效率上限的一种半理论半经验分析得出29%的结论；他同时所作一种基于黑体辐射平衡的理论分析得出效率上限在30%以上。有兴趣的读者可参阅本章所列其所著参考书。总体来看，30%应是对常温下硅晶太阳电池能量转换效率上限的较为稳妥的估计。

前面的分析中，我们未将光的反射、表面复合等列入自然局限因素。因为它属于业界不断努力克服的因素，虽然我们知道它不可能消失为零，但没有理论能给出一个下限。而温度、扩散、太阳光谱与半导体禁带特性这些都属于无可避免、相当“本征”的自然因素，至少到今天还是如此。

当然，技术发展无界，今天看来“本征”的局限，明天可能会被撼动。太阳光谱或可被某种上转换和下转换薄膜“修整”到更适合于太阳电池接受，实际上十多年前已有此类研究尝试；异质结和多结太阳电池亦能提高太阳光利用率，当然它没有改变半导体p－n结太阳电池效率受暗电流局限的本质。