太阳能光伏技术中的太阳电池等效电路与基本参数

如果将太阳电池p区和n区两端断开，前述载流子堆积过程将一直持续到两端表面，n区一端积累电子，p区一端积累空穴，直到不能再堆积为止。这时我们从两端可测到电压，这个电压称开路电压，Voc，以p区端为正，n区端为负。不难想象，这是太阳电池所能达到的最高电压。如果将太阳电池p区和n区两端短路，这时载流子流动完全畅行，电荷堆积消除，两端没有电压，这时太阳电池达到其所能达到的最大电流，称为短路电流，以电流密度计，Jsc。

以上两种情况下太阳电池都未对外做功，当电路上接入负载（电阻）后，太阳电池就对外输出一定电压和电流，注意这个输出电压对太阳电池作为一个p－n结二极管来说同时又是一个正偏压。其等效电路如图4．4所示。图中太阳电池的二重角色，光伏电源和二极管，被分开以两个并联元件表示。这是个颇令人遗憾的事实，因为光生电流Iph的一部份成为二极管正向电流Ii被分流了。即使理想太阳电池也不能避免，其输出电流I有

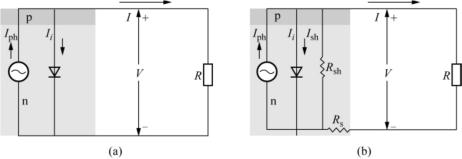
图4．4　半导体太阳电池等效工作电路图（图中所示为n型太阳电池）（a）理想电池　（b）实际电池

其中：Ii是已分出来的与光照无关的二极管暗电流，其I－V关系符合肖克莱（Shockley）方程式（3－24），式（3－25），将其代入即有

令电池对外短路（R＝0），此时V＝0，使Ii＝0，从而I＝Isc＝Iph。所以电池的短路电流Isc与光生电流Iph数量上相等。这对非理想电池也成立。

令电池对外断开，对于理想电池，此时恒有Ii＝Iph，其物理意义是：在该正向偏置电压下太阳电池p－n结的正向电流（暗电流）应恰好与光生电流相互平衡抵消。可依此得出

现在来分析光生电流Iph，仍以电流密度，即单位电池面积上的输出电流，Jph来衡量。因电流是连续一致的，我们以跨越p－n结的电流来代表Jph。由于无光照时p－n结已达成平衡无电流，所以我们只需考虑光照造成的增量。按4．2讨论，光照基本不造成跨越p－n结的扩散电流增量，扩散贡献可忽略不计，因此所求电流就等于光激发非平衡载流子在内建电场E驱动下的漂移电流，设非平衡载流子浓度为Δnph、Δpph，则有(www.xing528.com)

考虑一个跨越p－n结的单位截面积的体积微元，如图4．5所示，其中Δnph、Δpph由光激发载流子产生率G、载流子复合率还有流入和流出该体积微元的两种载流子数量守恒决定，稍作推导可得

图4．5　一个跨越p－n结的单位截面积、厚度为dx的体积微元中的载流子平衡情况及式（4－4）、式（4－5）、式（4－6）所依坐标示意图

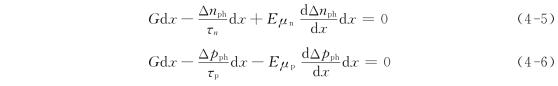
式中：Δnph／τn，Δpph／τp分别为单位体积内电子和空穴的复合率（见本书3．5）。

此类方程的求解一般需靠数值计算方法完成。马丁·格林［1］在忽略耗尽层复合损失、假定电池内部光生载流子产生率完全均一和假定p区与n区厚度可看作无穷大（无表面复合）的条件下，得出这个结果似乎意味着光生电流来自p－n结耗尽层和两侧扩散长度范围之内的材料中产生的载流子，有助于直观记忆，但并不能真的就认为它证实了光生电流与材料间有这样的来源关系，例如认为比电子扩散长度Ln小得多的n区厚度意味着失去了近一半光生电流；认为p区超过空穴扩散长度Lp的厚度部分就是浪费。

实际太阳电池的等效电路示如图4．4（b）所示。其偏离理想之处主要体现在两方面：一是电池材料或工艺缺陷难免导致一些漏电，以一个并联电阻Rsh代表，其值越小代表漏电越严重；二是串联电阻，电池正负极上金属与半导体的接触、栅线、还有对外接触，都难免引入电阻，以一个串联电阻Rs代表，其值越大电池输出损失越大。

太阳电池等效电路图使我们定量分析太阳电池运行参数十分直观便利，但是必须指出，理想太阳电池等效电路图本身是严格理论分析的产物，实际情况是先有式（4－2），然后有式（4－1），再有等效电路如图4．4（a）所示。因为等效电路图颇合我们的直觉想象，所以本章直接拿它来帮助我们在定性理解原理的基础上定量分析电池输出参数，以一张等效图代替了复杂冗长的推导，合乎本书宗旨。但饮水思源，读者需知它是来自理论推导，不是来自想象。