光伏技术应用中的p-n结特性

给一个自身已具有电压V0的器件外加一个电压V1，其结果很简单，如两者方向一致，器件上的电压就由V0增加为V0＋V1，如两者方向相反，器件上的电压就由V0减小为V0－V1。外加直流电压到p－n结两端时（习惯称偏置电压），由于p－n结空间电荷区载流子匮乏而电阻很高，而P区和N区各自都因有大量多数载流子而具备良好的电导率，因此外加电压将实际落在p－n结空间电荷区两端，与其自身已具备的自建电势VD相叠加。按一般习惯，以p－n结之P区为正极，N区为负极，以外加电压顺此极性为正向电压，记为Va，它与p－n结自建电势反向相反。因此外加电压Va后p－n结上的自建电势就将被替代为Vd－Va，如实际外加为反向电压，则相当于Va为负值。Vd改变为Vd－Va后，式（3－26）中Vd相应以（Vd－Va）替换后仍然成立；而I－V特性则随外加电压的方向不同而完全不同，分述于下。

Va为正，即外加正向偏压时，内建电势VD降低为VD－Va，内建电场减弱，从而使漂移电流减小，原有扩散电流与漂移电流之间的平衡被打破，p－n结有净扩散电流通过，其方向与外加电压方向一致。

Va为负，即外加反向偏压时，内建电势VD提高为VD－Va，从而使漂移电流增大，原有的平衡被打破，p－n结有净的漂移电流通过。此时的特点是电流依靠少数载流子的扩散维持，因为电场在p区将电子驱向n区，在n区将空穴驱向p区，有限的少数载流子需靠内部向电场作用区的扩散来维持提供，少数载流子浓度本已极低，其浓度梯度将很小，因此扩散供应相对电场驱动的漂移很慢，成为电流控制因素，电流很小，而且基本不随电压升高而增大。

肖克莱（Shockley）完成了以上定性描述的计算定量处理，得出p－n结的I－V关系如下

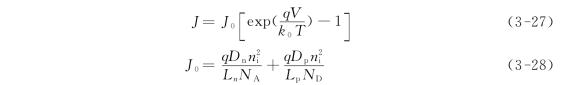
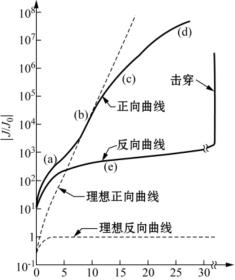
图3．12　理想的晶体硅p－n结J－V关系曲线（虚线）及实测曲线（实线）［7］(www.xing528.com)

式中：J为单位面积横截面上的电流I，即电流密度；V即为前述之Va；Ln，Lp分别为电子和空穴的扩散长度

计算中沿

用了前面采用的简化近似，而且未考虑过程中载流子的复合造成的电流损失，也未考虑光照激发导致的载流子产生（故所得电流称为“暗电流”）。图3．12画出了式（3－27）、式（3－28）代表的I－V关系（虚线）。可以看到反向偏压条件下p－n结的反向电流密度随反向电压增大而趋于稳定饱和，称为反向饱和电流密度。令式（3－27）中V趋向于负无穷大，得到J趋于－J0，因此反向饱和电流密度即为J0。

实际硅半导体p－n结的测量I－V曲线特征（见图3．12实线）与肖克莱方程曲线（见图3．12虚线）之间有所差别。如实际反向电流更大，原因是推导中未计入势垒区（空间电荷区）热激活产生的载流子被强电场驱离而脱离平衡复合的部分（本来平衡时热激活与复合相互完全抵消）；正向电流也还有由复合带来的贡献未计入：正向偏压条件下大量电子和空穴分别由n区和p区扩散注入势垒区，它们相互复合抵消的结果应形成一股额外的电流，称为复合电流，理论证明复合电流与exp（qV／2k0T）成正比，而纯扩散电流与exp（qV／k0T）成正比；最突出的差别是实际p－n结反向电压加到一定程度后，反向电流突然增大，称为击穿。击穿电压随掺杂浓度增大而下降。硅半导体p－n结的击穿电压一般在几伏到上百伏范围。击穿机制与前述各种物理过程完全不同，在正常工作范围对太阳电池光伏性能亦基本无影响，此处不再进一步介绍。

以上分析和结果均基于均匀的p、n区成分与突变的p－n结。实际的p－n结中掺杂成分多少是渐变的，对它们的分析更为复杂，但最终分析结果与以上所得是一致的，并且为实验结果所证实。这对于光伏电池技术有很大意义，因为采用扩散制结成本较低，而理论分析显示扩散所得渐变过渡的掺杂结构依然能具备p－n结的功能。下一章中我们还将通过数值计算分析看到，扩散p－n结的太阳电池的发电效能其实不逊于突变p－n结的太阳电池。