太阳能光伏技术中的p-n结内建电场

考虑一个如图3．9所示的p－n结，假定体系在各个方向的尺度都可以看作无穷大，分析中不涉及表面局限。现设想该p－n结瞬间形成之后初期将发生的微观过程和导致的结果，可归纳为三个要点：

1）扩散

n型区电子浓度较p型区高，电子会由n型区向p型区扩散；同样空穴会由p型区向n型区扩散。这两种扩散的共同点是多数载流子从p－n结的一侧流向另一侧成为少数载流子，增加另一侧少数载流子的浓度。注意物质上这两个扩散都是电子的扩散，但一个是导带的自由电子、一个是价带的成键电子，后者扩散率较低。

2）电场产生

体系两侧材料原本都是处处电中性的，以上载流子扩散迁移的结果，使得留下的区域必然带上与迁移离去的电荷符号相反、数量相等的电荷。对图1情况而言，就是在p－n结附近p型区中留下无空穴与之中和的B－离子，附近n型区中则留下无电子与之中和的P＋离子。应该指出，这些离子本来都已存在并分布在p－n结两侧，所不同的是现在与之平衡的电荷（载流子）迁走了；这些离子不会发生扩散迁移或漂移，它们取代硅原子处于晶体金刚石点阵位置，只有1 000℃左右的高温才能使之发生可观迁移。这些荷电性质相反的离子分布在p－n结两侧附近，自然构成一个由n型区指向p型区的电场，称为内建电场。

3）平衡

不难看出，以上由扩散所导致的电场将抵抗上述两种载流子扩散；然而随扩散进行，该电场又不断加强，从而对扩散的抵抗不断加强，最终达成稳定平衡。稳定平衡的含义是即使有任何微扰使之偏离平衡，体系亦能自发回到平衡状态。

以上过程应在极短时间内就可完成，实际只能存在于假想之中；制备完成后到我们手上的p－n结，必然是已经处于上述平衡状态下。此时p－n结附近载流子扩散流失几尽，称为耗尽层，注意不可能彻底“耗尽”，因平衡热激发还在，浓度积pn恒定还须保持；耗尽层内掺杂离子使p－n结两侧各带相反电荷，称为空间电荷区；这也正是内建电场作用区。这个区层因极其重要而被从不同角度赋予不同名称，读者当注意汲取其物理含义，加深理解，而不是相反为其多重名称所困惑。

图3．9表示了上述要点之1）和2），平衡则尚难于图示。必须指出，p型区耗尽层之外同样有B－离子，只不过它们都被空穴平衡而不带电荷，因此未把它们画出来，以示区别；同理未把n型区耗尽层之外的P＋离子画出来。

清楚了以上要点以后，了解p－n结内建电场强度、内建电势、载流子浓度分布、空间电荷区宽度等就基本上只是数学求解问题了。基本的方程即为对上述平衡的

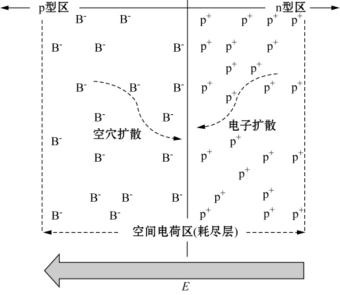
图3．9　p－n结及内建电场E形成示意图

表述：平衡时两种载流子的净流量均处处为零（Jn（x）＝0，Jp（x）＝0），即电子的扩散流量与内建电场作用下电子的反向漂移流量处处相等，空穴的扩散流量与内建电场

作用下空穴的反向漂移流量处处相等；由这可导出体系各处的费米能必均等，这样一来p－n结体系能带结构必发生如图3．10所示弯折。远离p－n结处的p型硅和n型硅中，材料的费米能应不变，更准确地说，其费米能相对其价带顶与导带底的位置应不变，n型硅中费米能位置相对较高；p型硅费米能位置相对较低。观察图3．10可知，在空间电荷区能带发生这样的弯折是唯一能够同时满足费米能处处均等、而又在远离p－n结区域材料能带结构中保持正确相对位置的方式。这种弯折也体现了内建电场的作用。容易看出，弯折量，即内建电势能qVD，即为弯折前n型硅中费米能Efn与p型硅中费米能Efp之差，由此得到内建电势VD有(www.xing528.com)

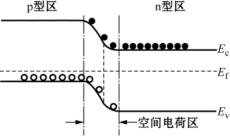
图3．10　p－n结电子能带结构示意图

式中：VD亦被称为p－n结接触电势差，qVD亦被称为p－n结势垒。由上式可推得

代入ni式（3－4）可进一步得可以看到VD为材料的禁带宽度Eg折算为电势差后，减去一个与两部分材料掺杂浓度积有关的项，这项一般大于零，随此浓度积增大而向零接近，使VD较高。

平衡条件下p－n结中载流子浓度的分布，应该同样满足式（3－2）、式（3－3），只是其中Ef与Ec或Ev之差值不再是处处均恒，而是在空间电荷区有相应于图3．10所示能带弯折的变化，如此所得电子与空穴浓度分布将具有图3．11所示形状，平衡条件下（无热激发以外的其他激发）它满足在任一x坐标位置，p（x）n（x）＝n2i。该图系采用一种太阳电池数值模拟软件（PC1D，具体介绍见第4章）对一种晶体硅p－n结计算得到，其结构与p型硅衬底太阳电池的p－n结类似。

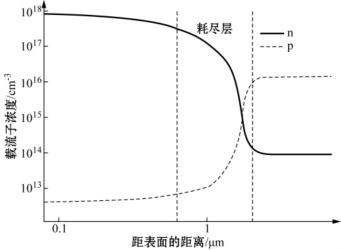
图3．11　晶体硅p－n结附近电子浓度n与空穴浓度p的对数的分布

（PC1D计算结果）

假定空间电荷区电荷密度均一，在P型区和N型区深度分别为Wp、Wn，它们的总电荷应分别平衡从该区扩散移出的载流子的电荷，可以估算得出由于内建电势VD已由半导体禁带宽度和两侧掺杂浓度确定，Wp、Wn的大小将决定内建电场的强度。