横截面积相同的管子(环形截面积)和实心杆两个相比较,管子在强度上有什么突出的优点吗?如果是就抗压和抗断的强度方面来谈这个问题,管子可以说毫无优点,要压裂和拉断管子和实心杆所需的力量是一样的。可是在抗弯方面,它们就不一样了。要把一根管子弄弯曲,与弄弯曲一根和它横截面积相同的实心杆相比,所需的力量要大得多。
很久以前,为强度科学奠定基础的伽利略对这一点就曾说过一段精辟的话。我要在下文中引用伽利略在《关于两门新科学的谈话和数学证明》中的一段话,希望读者可以理解我对这位在科研方面有着突出贡献的学者的偏爱。
对有关非实心物体抗力强度的意见,我还要说几句,这种非实心的固体一直都在被我们人类的技艺(技术)和大自然利用着。这种物体想要增加自己的强度可以不必同时增加自己的重量,鸟类的骨头和芦苇就是在这一点上的最好见证。虽然它们都没有太大的重量,但是抗弯和抗断力都很强。麦穗的重量要比麦秆的重很多,但是仍然被麦秆所支撑。假如用相同重量的实心麦秆所代替,那它就不会有这么大的抗弯和抗断力。非实心的棒子和木头还有金属管子的强度,要比同样重量实心的物体高好多,但是非实心和实心相比较要粗很多,这一点是人们早就发现并用实验证实了的。这个结果被人类的技艺应用到了很多东西的制造上,用空心制造的这些东西既轻巧又耐用。
要弄懂空心物体的坚硬度为什么会比实心的大,我们首先要对大梁在弯曲的时候会产生什么样的应力来进行一下研究。如图7-4,一个两端AB 被支起的梁,重力Q 作用在中间。这时发生的变化是,梁在这个重力Q 的作用下变得弯曲了。因此梁的下部被拉伸了,上部被压缩了,而处在中间的一层,我们可以称之为中间层,无论是拉伸还是压缩都没有影响到它。这个时候就会在下部和上部同时产生反拉伸和反压缩的弹性力,这个力努力想使梁恢复原来的形状。在弹性极限允许的范围内,这个弹性力会随着梁的弯曲程度的增加而增大。什么时候这个弹性力和力Q 分解的压缩和拉伸力相等了,梁就会停止弯曲。
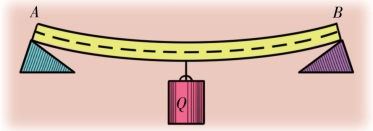
图7-4 被压弯的梁
经过分析我们知道,梁的最上层和最下层抗弯曲的作用力最大,越是向中间层靠近,这个抗弯曲的作用就越小。
所以要使梁的强度有所增加,就要使组成材料远离中间而靠向两边。例如,工字梁和槽梁(图7-5)的组成材料就是这样分布的。(https://www.xing528.com)
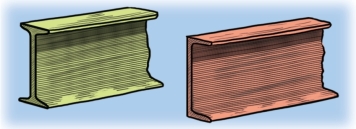
图7-5 工字梁和槽梁
桁架[2]在节省材料这方面要比工字梁做得更加到位。因为中间几乎全部的材料都被除去了,用杆AB 和CD 连接着杆a、b、c、……、k 替代,所以桁架(图7-6)非常轻便。由上面的内容读者可以知道,在负重F1 和F2 共同作用下,AB 被拉伸,而CD 被压缩。
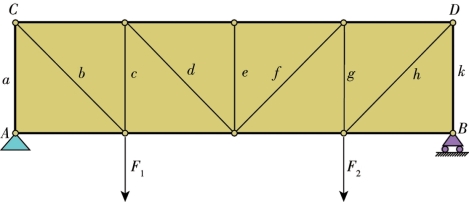
图7-6 桁架构造图
通过上述原理,管子为什么要比实心杆抗弯能力强,读者应当清楚了吧。我们再用数字来说明一下。这里有一根管子和一根同它长短相同的实心圆梁。管子的环形截面积和实心梁的横截面积相等。它们当然有着相同的重量,可是两者的抗弯力是不一样的。我们可以通过计算得知,管子梁[3]的抗弯力比实心梁大一倍多,大约大112%。
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




