小球挣脱向心力束缚的原因及公式推导

如果要更好地理解后面的一些定义，我们可以先看下面的例子。

在一个非常光滑的桌面上，钉一颗钉子，然后用细线拴一个小球（图5-1）。用力给小球一个速度v，小球首先会在惯性作用下作直线运动，直到细线被拉直，再后来它会一直以钉子为圆心、细线为半径，不停地作圆周运动。小球的细线假如被火烧断（图5-2），它就会在惯性作用下沿圆周的切线方向飞出去。这就好比在一个高速旋转的磨刀砂轮上，磨刀飞出的火星，这两个情景非常相似。小球之所以挣脱了向心力的束缚进行直线运动，是因为没有了细线的牵扯力。由牛顿第二定律，加速度和作用力的方向一致，大小是成正比的。所以，小球在细线牵扯力的作用下就会有一个指向圆中心（也就是钉子）的加速度。我们把这个牵扯着小球一直围绕圆心运动，使它不能随自己的惯性向远处飞去的力，叫作向心力，把由它所产生的加速度称作向心加速度。

图5-1　小球的圆周运动

图5-2　断线后，小球沿切线方向运动

假设细线的长度是R，小球的圆周运动线速度是v，那么向心加速度根据牛顿第二定律，得出向心力：

再让我们推导一下向心加速度的公式。如果小球在圆周运动过程中的A 点时，细线被烧断。在惯性作用下，小球就会在A 点沿着圆的切线飞出去。假如它到达B 点所用的时间是t（图5-3），那么这一段的距离就是AB=vt。但是如果小球是在向心力的作用下作圆周运动，它在t 时间里到达的是C 点。再由C 点作OA 的垂直线CD，它的长度就是和向心力等值的力量作用在小球的上面使小球走出的距离。这可以根据初速度为0 的匀加速运动的公式求得：

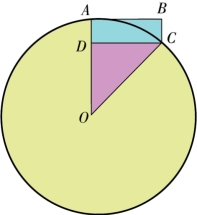
图5-3　向心加速度的公式推论

(www.xing528.com)

公式中的a 表示向心加速度。再根据直角三角形性质可以推出：

OC2=OD2+DC2

CD=AB=vt

推出：

又推出：

最后得出：

这只是小球在非常短的时间（小到几乎没有时间）里的运动，所以，与Ra 和v2相比较，的大小就可以忽略不计。于是，我们就可以推论出：