三颗铁球同时放置的实验结果

在一堵直立的墙面上画一个直径1 米的大圆圈（图4-7），然后把两个滑槽顺着顶点A 装好。在顶点A 处同时放三颗铁球，其中的两颗沿着滑槽滑落（假设没有摩擦和滚动），另一颗垂直降落。请回答，最先到达圆周的是哪一颗？

大多数人都会认为滑槽AC 里的铁球会最先到达，因为AC 距离最短；然后第二名会是AB 滑槽里的铁球；而垂直降落的铁球会最晚到达。

可是，实验证实这三颗铁球到达的时间是一致的，上面分析的结论是不正确的。

实验分析可知：三颗铁球的运动速度是有区别的，其中垂直降落的铁球速度最快，其余两颗铁球在AB 中的要比在AC 中的速度快，因为滑槽AB 要比AC 陡峭。综上所述，有的铁球虽然路程较远，但是它的速度更大，这增加的速度对远出的路程正好是个很好的弥补，这一点我们可以通过计算来证实。

其实，在忽略大气阻力的情况下，我们可以通过公式：

求出垂直方向降落的时间t，得出：

滑槽中的运动时间，以滑槽AC 为例，可得出t1 为：

其中的a 代表滑槽AC 中的加速度。我们可以很轻松地得出：

由此推出：

根据图4-7可以得出：(www.xing528.com)

由此推出：

即可得出：

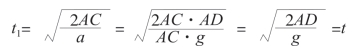
最后答案就是t1=t，所以说滑槽中的铁球和垂直降落的铁球所用时间相等。以滑槽AC 推出的结果，其实适用于所有在A 点引下来的滑槽。

上面题目的说法其实还有另外的一种形式。如图4-8，在一个竖直的平面上，分别在A、B、C 三点同时放上三个物体，使它们在重力作用下分别沿着AD、BD 和CD 方向运动。请问第一个到达D 点的是哪一个？

这三个物体会在同一时间到达，对于这一点读者此刻可以轻松地得出结论。

伽利略在《关于两门新科学的对话》一书中，第一个提出了这个物体落下的题目，而且做出了详细的解答。

图4-7　

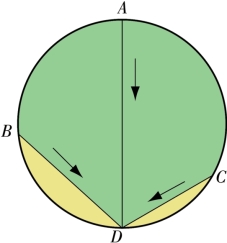
图4-8　伽利略的题目

关于伽利略对这个现象总结的定律，我们可以从这本书里读到：“如果在地平线之上某一个竖直圆圈的最高顶点上，向圆周引出不同的斜面，物体通过这些斜面从顶上滑到圆周处，所需的时间相等。”