跳球实验结果揭示了跳高运动员的潜力

七里靴是童话故事里的一种靴子，如今却被人们以一种特别的方式变成了现实：一套氦气供应设备加一个形体不大的气囊（气球被放在里面），还有一个可以盛放它们的规格差不多的旅行箱。这个气囊可以随时被运动员从皮箱里取出来使用，只要给它充满氦气，它就会变成直径5 米的气球。运动员可以利用这个气球跳特别远的距离（图4-1）。这个气球在空气中受到的浮力，没有人体重量大，所以我们不必担心自己会飞到高空去。

图4-1　跳球

让我们做一件有趣的事情，那就是算一下这个运动员假如利用了这个气球，他能跳到的高度是多少？

我们可以假定气球的浮力比人体重力小1 千克力，也就是说，人如果用了这个气球，它的体重好像只剩下1 千克了。如果正常的体重为60 千克，请问他所跳出的高度会不会是原来的60 倍？

我们应当这样算：

人利用气球后重力只剩下了1 千克力，大约是10 牛顿。气球自身的质量约为20 千克。也就是说，有20+60=80 千克的物体受到10 牛顿力的作用，它所得到的加速度a 用公式可以算出：

在不用气球的情况下，人在原地蹦高不会超出1 米。他的相对速度v 由公式：

v2=2gh

可得：

v2=2×9.8 米2/秒2

算出v 大约是4.4 米/秒。人身上系着气球时跳起的速度一定会比不利用气球时小，两个速度的比值应当是60∶80。由公式Ft=mv 就可以推出这一点，在力F 和作用时间保持不变的情况下，也会产生相同的动量；换句话说，速度与质量成反比。根据比值，可以求得身上系着气球跳高的速度是：

再根据公式v2=2ah，代入相关数据，得：

3.32=2×0.12×h

得出h 大约是45 米。因此，运动员用自己普通情况下跳1 米的力量，在利用气球时就可以跳出45 米的高度。

其实这种情况下跳跃时间的计算也非常有意思。把利用气球跳出的高度45 米和加速度0.12 米/秒2 代入公式：

求出：

跳上去还要落下来，总共需要54 秒的时间。(www.xing528.com)

加速度比较小是这个跳跃花费时间长的主要原因。假如不是利用了气球，那就要在比地球的重力加速度小近60 倍的其他小行星上，我们才可以体会到这种跳高的感觉。

当然我们是在不计空气阻力的情况下作以上计算的，下面遇到的计算也是一样的。可是我们要明白，即使把空气阻力计算在内，跳出的高度和所需的时间运用力学理论里面的一些公式也是可以计算出来的。只是在这样的情况下和在真空中相比，跳出的高度和所需的时间要小许多。

对于他究竟可以跳出多远，我们也可以来算一下。运动员在跳远时他跳出方向和地平线应当有一个角度α。让我们假定他的初速度为v（图4-2），它由两部分组成：垂直起跳速度v1 和水平方向的速度v2。三者的关系式为：

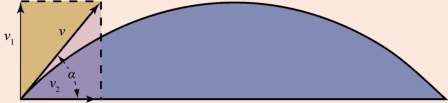
图4-2　把物体沿和水平线成一定角度的方向抛出的线路

v1 =v×sinα

和v2 =v×cosα

设人体的运动时间为t，即可以得出：

v1－at=0 或者v1=at

推出：

得出人体的跳远所需时间：

水平方向的速度v2 在整个的过程中应当是保持不变的，人体在水平方面匀速向前，那么2t 时间里移动的距离是：

所有正弦值都要小于或是等于1，所以sin2α=1 的时候，s 最远。也就是说，2α=90°即α=45°时s 值最大。所以，在不计大气阻力的情况下，运动员只有以45°角的方向跳，才会跳得最远。至于最大的距离，可以把v=3.3 米/秒、sin2α=1、a=0.12 米/秒2等数值代入公式就可以了。

利用气球，我们可以跳过几层楼高呢？（图4-3）^[2]

图4-3　利用跳球的跳跃

我们自己也可以用一个孩子们玩耍用的氦气球和一个比它的漂浮力重一点的玩具运动员，来做这样一个实验。小运动员会在我们轻轻一碰的情况下就起来，然后再缓缓落下。但是它的空气阻力一定会比真人要大，所以速度会小很多。