周期为2π的函数的傅里叶级数展开为实用微积分中的结果

三角级数在电路分析与设计、电子信号处理中有着广泛的应用，假定f（x）能展开成三角级数式（7-10）.下面讨论三个问题：

（1）如何求系数a0，an，bn；

（2）周期函数f（x）满足什么条件，可以展开成三角级数；

（3）展开的三角级数的收敛情况.

对于第（1）个问题：如何求系数a0，an，bn？

法国数学家傅里叶利用三角函数系的正交性，找出计算a0，an，bn的公式，从而以他的名字命名了傅里叶系数与傅里叶级数.

设f（x）是周期为2π的函数，如果

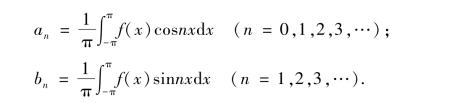
存在，则称它们为函数f（x）的傅里叶系数，由傅里叶系数组成的三角级数

称为傅里叶级数.

下面我们给出一个收敛定理，它将得出上述第（2）、第（3）问的重要结论.

收敛定理[狄利克雷（Dirichlet） 充分条件] 设周期为2π的函数f（x）满足条件

（1）在区间[ -π，π]连续或只有有限个第一类间断点；

（2）在区间[ -π，π]只有有限个极值点.则函数f（x）的傅里叶级数收敛，且

当x是连续点时，级数收敛于f（x）；

当x是间断点时，级数收敛于

由于收敛定理的条件，对初等函数与实际问题中的分段函数一般都能满足，因此傅里叶级数具有广泛的应用性.

【例1】 脉冲矩形波的信号函数f（x）是以2π为周期的函数，它在[ -π，π]的表达式为

图7-1

如图7-1 所示，求此函数的傅里叶级数展开式.

解 用傅里叶系数公式计算傅里叶系数如下.

因为函数f（x）是奇函数，所以f（x）cosnx是奇函数，因此f（x）cosnx在（ -π，π）上积分为零.于是

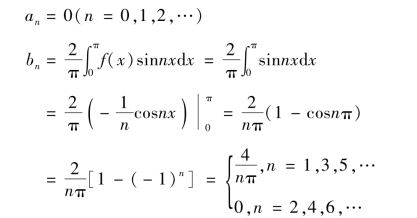
于是，函数f（x）的傅里叶级数展开式为(www.xing528.com)

由收敛定理知函数f（x）在-∞＜x＜+∞，x≠kπ，k=0，±1，±2，…

内与级数相等，即

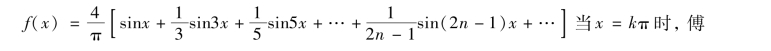
里叶级数收敛于

图7-2

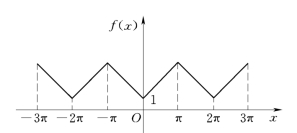
图7-3

此函数的傅里叶级数收敛情况如图7-2 所示，从图7-1 与图7-2 可以比较出函数f（x）与其傅里叶级数的差异.

【例2】 已知脉冲三角信号f（x）是以2π为周期的函数，它在[ -π，π] 的表达式为

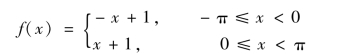
如图7-3 所示，将函数f（x）展开成傅里叶级数.

解 因为函数f（x）是偶函数，所以f（x）sinnx是奇函数，因此它在（ -π，π） 上积分为零.于是

由于函数f（x）在（ -∞，+∞）上连续，所以

【例3】 无线电设备中，常用电子管整流器把交流电换为直流电，已知电压u（t）与时间t的关系为u（t） =|sint|，试将它展开为傅里叶级数.

解 函数u（t）的图形如图7-4 所示，它满足收敛定理的条件，且在整个数轴上连续，因此它的傅里叶级数处处收敛到u（t）.

因为函数u（t）是偶函数，所以bn=0 （n=1，2，3，…）

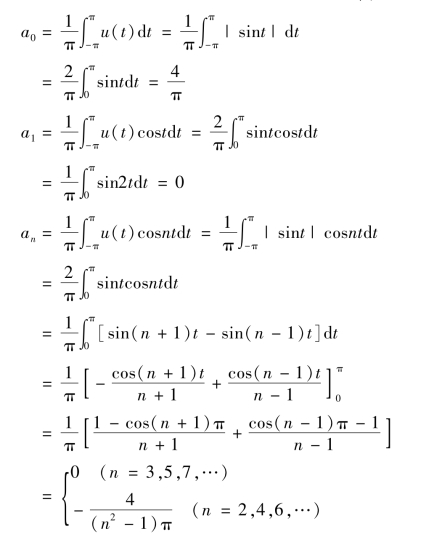
图7-4

所以u（t）的傅里叶级数展开式为