微积分实际应用：二重积分在物理领域的应用

1.平面薄板的质量

设有一平面薄板，占据xOy平面上的某个有界闭区域D，并设薄板在任意一点（x，y）处的面密度为ρ（x，y），且ρ（x，y）在区域D上连续，则平面薄板的质量为

【例4】 有一个等腰直角三角形薄板，腰长为a，各点处的面密度等于该点到直角顶点距离的平方，求此薄板的质量.

解 如图6-41 所示建立坐标系，则斜边AB的方程为x+y=a，薄板所占的区域D为

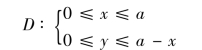
据题意，在区域D上任意一点（x，y）处的面密度为

图6-41

所以，该薄板的质量M为

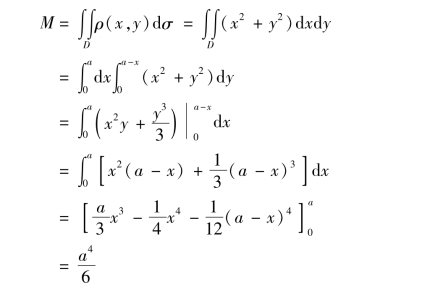
2.平面薄板的重心

设平面薄板占有xOy平面上的闭区域D，D内任意一点 （x，y） 处的密度函数ρ（x，y），且ρ（x，y）在D上连续.在D上任取一个面积微元dσ（也表示该小区域的面积），取（x，y） ∈dσ，则该小薄板的质量微元为

将此质量微元的质量看作集中在点（x，y）处，则对x轴、 y轴的静力矩微元分别为

所以该薄板关于x轴、 y轴的静力矩分别为

如果薄板是均匀的（即ρ（x，y）为常数），面积为S，则

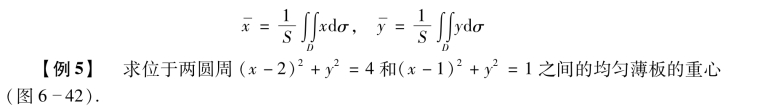
解 根据题意，积分区域D在极坐标系中可以表示成

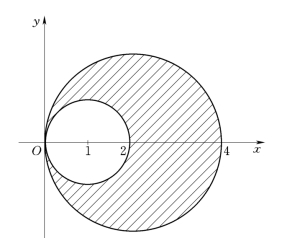(www.xing528.com)

图6-42

二重积分的应用非常广泛，自然科学、工程技术中许多问题都可以转化为二重积分这种数学模型来解决.我们列举了一些几何方面与物理方面的实例，不求全面，旨在增强读者运用二重积分解决问题的能力.

习 题6-6

3.设平面薄板所占区域D是由直线x+y=2，y=x和x轴所围成，它的面密度ρ（x，y） =x2+y2，求该薄板的质量.

4.设半径为1 的半圆形薄板上各点处的面密度等于该点到圆心的距离，求此半圆的重心.

复习检测题六

1.填空题.

2.选择题.

（1）点（1，1，1）关于原点的对称点为（ ）.

（A） （1，1，-1）； （B） （ -1，-1，-1）；

（C） （ -1，1，-1）；（D） （ -1，-1，1）.

（A）旋转抛物面；（B）圆柱面；

（C）圆锥面；（D）球面.

3.求下列函数的定义域.

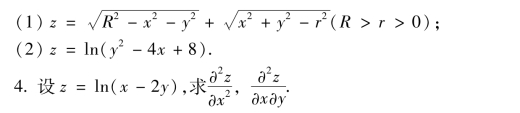
5.求下列函数的极值.