空间曲线的坐标面投影

定义5 设Γ为已知的空间曲线，以Γ为准线，母线平行于z轴的柱面∑称为Γ关于xOy坐标面的投影柱面；∑与xOy面的交线C称为Γ在xOy面上的投影（图6-15）.

类似地，可以定义Γ关于yOz（或zOx）坐标面的投影柱面和Γ在yOz（或zOx）面的投影.

设曲面∑1、∑2的方程分别为F（x，y，z） =0，G（x，y，z） =0，Γ为曲面∑1与∑2的交线，曲线Γ的一般式方程为

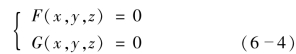
消去z，得

满足曲线Γ的方程（6-4）的x，y，z必定满足方程（6-5），所以H（x，y） =0 是Γ关于xOy坐标面的投影柱面（∑）方程，从而

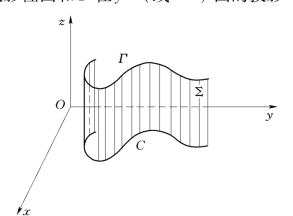
图6-15

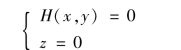
表示Γ在xOy面上的投影曲线的方程（图6-16）.

同理，由式（6-4），消去x得R（y，z） =0，消去y得S （x，z） =0，则曲线Γ在yOz、 zOx坐标面上的投影曲线的方程分别为

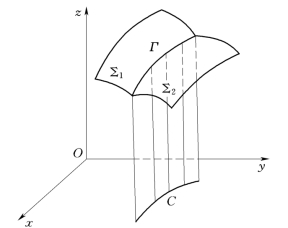
图6-16

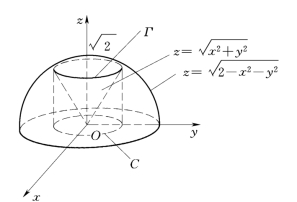
图6-17

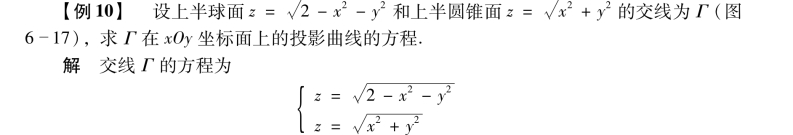(www.xing528.com)

消去z，得Γ关于xOy坐标面的投影柱面x2+y2=1，从而交线Γ在xOy面上的投影曲线C的方程为

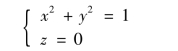
练 习6-1

1.在空间直角坐标系中作出下列各点：

A（2，-1，3）；B（ -2，-3，1）；C（1，2，-3）；

D（0，0，2）；E（ -2，0，0）；F（0，-1，0）.

习 题6-1

1.在空间直角坐标系中，作点A（3，1，2） 和点B（2，-1，3） 并写出它们分别关于三个坐标面、三条坐标轴、原点的对称点的坐标.

2.在x轴上求一点，使它到点（ -3，2，-2）的距离为3.

3.求到点（ -4，3，4）的距离等于到xOy平面的距离的动点的轨迹方程.

4.求球面x2+y2+z2-2x+4y-4z-7 =0 的球心与半径.

5.指出下列各方程所表示的曲面.

（1） 3x2+4y2=25；（2） 5x2-6y2=10；

（3） 3x2=8y； （4） z2-x2=1.

6.yOz面上的曲线y2=z绕z轴旋转一周，求此旋转曲面的方程.