微分方程在自然科学及工程技术中有广泛的应用,这一节主要介绍一阶、二阶微分方程在几何、物理等方面的一些应用.本章第一节已归纳出利用微分方程解决实际问题的一般步骤,下面通过例题加以说明.
【例1】 某水塘原有50000t清水(不含有害杂质),从时间t=0 开始,含有有害杂质5%的浊水流入该水塘,流入的速度为2t/min,在塘中充分混合(不考虑沉淀) 后又以2t/min的速度流出水塘.问经过多长时间后塘中有害物质的浓度达到4%?
解 (1)建立微分方程.

(2)求通解.

【例2】 牛顿冷却定律指出:物体在空气中冷却的速度与物体温度和空气温度之差成正比,现将牛顿冷却定律应用于刑事侦察中死亡时间的鉴定.当一次谋杀发生后,尸体的温度从原来的37℃按照牛顿冷却定律开始下降,如果两个小时后尸体温度变为35℃,并且假定周围空气的温度保持20℃不变,试求出尸体温度H随时间t的变化规律.又如果尸体发现时的温度为30℃,时间是下午4 点整,那么谋杀是何时发生的?
解 (1)建立微分方程.
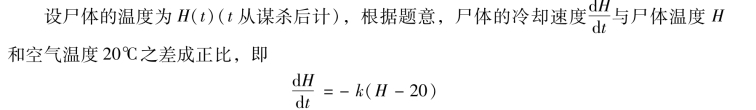
其中k>0 是常数,初始条件为H(0) =37.
(2)求通解.
分离变量得
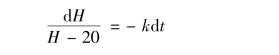
积分得
![]()
(3)求特解.
把初始条件H(0) =37 代入通解,求得C=17,于是该初值问题的解为
![]()
为求出k值,根据两小时后尸体温度为35℃这一条件,有

![]()
【例3】 如图5-2 所示,这是一个由电阻R,电容C和直流电源E串联而成的电路.已知在开关K闭合前电容C上没有电荷,电容C两端的电压为零,电源电压为E.当把开关闭合上,电源对电容充电,电容C上的电压UC逐渐升高,求电压UC随时间t变化的规律.
解 设在时刻t,电容器两端的电压为UC,电阻两端电压为UR,电路中的电流为I.由回路电压定律知
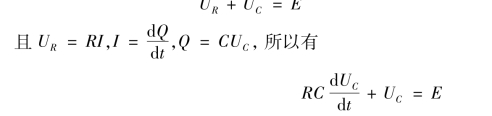
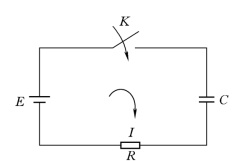
图5-2
这是一个一阶非齐次线性微分方程,初始条件为UC(0) =0 容易求得它的通解为
![]()
将初始条件代入,得C=-E,因此
![]()
这就是电压UC随时间t变化的规律,即电容器的充电规律,显然,由图5-3 看出,充电时UC随t增加而增加,最后稳定在UC=E.

图5-3
【例4】 列车在平直线路上以20m/s的速度行驶,当制动时列车获得加速度-0.4m/s2,问开始制动后多少时间列车才能停住,以及列车在这段时间里行驶了多少路程?
解 设列车在开始制动后t秒内行驶了s米,按题意,欲求出未知函数s=s(t).已知加速度

![]()
即列车开始制动后50s停住,在这段时间里共行驶了500m.
【例5】 在地面以初速度V0垂直向上射出一物体,设地球的引力与物体到地心的距离的平方成反比,求物体可能达到的最大高度.(空气阻力不计,地球半径R=6370km)
解 取坐标系如图5-4 所示,原点取在地球表面,因物体射出后,在运动过程中仅受地球引力F的作用,而
![]()
其中s是物体与地面的距离,k为比例系数.
现在先求常数k,显然,当物体在地面时,s=0,F=mg,m为物体的质量,因此由式(5-41)得k=mgR2,于是
![]()
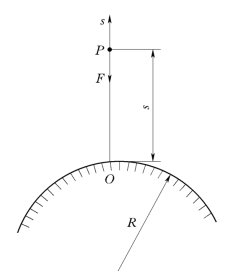
图5-4(https://www.xing528.com)
根据牛顿第二定律,物体的运动方程为
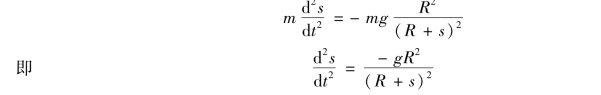
这是可降阶的不显含自变量的二阶微分方程.
由题设有初始条件s|t=0=0,s′|t=0=V0,

故得最大高度

这个速度就是通常所说的第二宇宙速度.
练 习5-4
1.有高为1m的半球形容器,水从它底部的小孔流出,小孔横截面积为1cm2(图5-5),开始时容器盛满水,求水从小孔流出过程中容器里水面的高度h(水面与孔口中心间的距离)与时间t的函数关系(已知水从孔口流出t秒时的流速![]() 其中V为水从孔口流出t秒的体积,s为孔口横截面面积).
其中V为水从孔口流出t秒的体积,s为孔口横截面面积).
2.一质量m=10kg的物体被系于一劲度系数k=20kg/s2的弹簧上,这一物体受到与运动速度成正比的摩擦力的作用,比例系数h =20kg/s,在时刻t=0,物体被从高2m的地方从静止状态自由放开,(1)试写出描述这一运动的微分方程;(2)求运动规律.

图5-5
习 题5-4
1.已知曲线过点(1,2),且曲线上任一点M(x,y)处切线的斜率是该点横坐标的倒数,求此曲线方程.
2.一容器内盛有50L的盐水溶液,其中含有10g的盐,现将每升含盐2g的溶液以每分钟5L的速度注入容器,并不断进行搅拌,使混合液迅速达到均匀,同时混合液以3L/min的速度流出溶液,问在任一时刻t容器中含盐量是多少?
3.降落伞张开后下降,设所受空气阻力与降落伞的下降速度成正比例,且伞张开时(t=0)的速度为0,求降落伞下降速度υ与时间t的函数关系.
4.在一个含有电阻R、电容C和电源E的RC串联回路中,由回路电流定律,知电容上的电量q满足以下微分方程
![]()
若回路中有电源400cos2tV,电阻100Ω,电容0.01F,电容上没有初始电量,求在任意时刻t电路中的电流.
5.设一弹簧放于油中,其运动满足微分方程
![]()
设初始条件为s|t=0=-0.5,s′|t=0=3,求微分方程的特解.
6.一质点在一直线上,由静止开始运动,时刻t时质点的位置为s(t),其加速度a=-4s(t) +3sint,求运动方程,并求离起始点的最大距离.
复习检测题五
1.选择题.
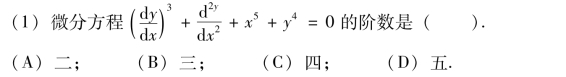
(2)下列微分方程中属于二阶常系数非齐次线性微分方程的是( ).
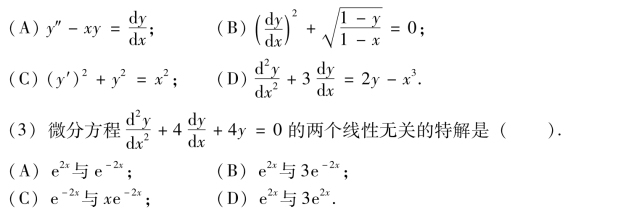
(4)微分方程2y″+3y-4 =0 对应的齐次方程的特征方程是( ).
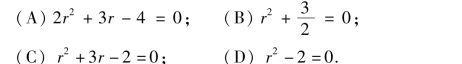
(5)下列微分方程中属于可分离变量微分方程的是( ).
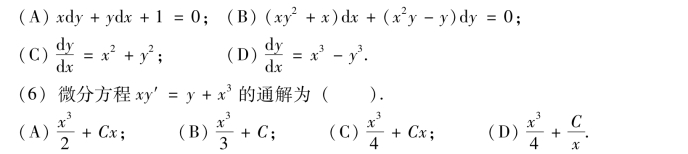
(7)微分方程y″+3y′-18y=x2e3x的特解形式为( ).
(A) ax2e3x;(B) ax4e3x;(C) x(ax2+bx+c)e3x;(D) x2(ax2+bx+c)e3x.
(8)设y1、 y2为某二阶常系数齐次线性微分方程的解,那么y=C1y1+C2y2(C1、C2为任意常数)是方程的( ).
(A)解;(B)通解;(C)特解;(D)全部解.
2.求下列微分方程的通解.
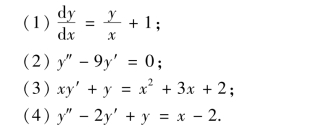
3.求下列微分方程满足初始条件的特解.
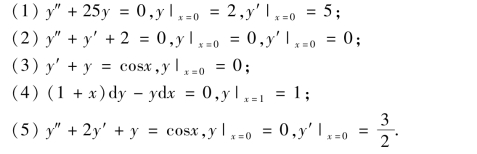
4.已知二阶常系数齐次线性微分方程的特征根为r1=-1,r2=3,求此微分方程.
5.已知某曲线经过点(1,1),它的切线在纵轴上的截距等于切点的横坐标,求它的方程.
6.一潜艇质量为m,由静止开始沉入水中,下沉时的阻力与下沉的速度成正比,求潜艇下沉的深度与时间的函数关系.
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




