实用微积分：解二阶非齐次线性微分方程

二阶常系数线性非齐次微分方程的一般形式为

其中p，q为常数，f（x）为已知函数.

由定理3 可知，求二阶常系数线性非齐次微分方程的通解，可以先求对应的线性齐次方程y″+py′+qy=0的通解Y，这个问题已解决；其次，是求出二阶常系数线性非齐次方程（5-30）的特解y*，如果y*求出，那么方程（5-30）的通解为y=Y+y*.因此关键问题是如何求方程（5-30）的一个特解，下面讨论求方程（5-30）的一个特解y*的方法.

（1） f（x） =pm（x）eλx（其中λ是常数，pm（x）是x的一个m次多项式）这时方程（5 30）可写成

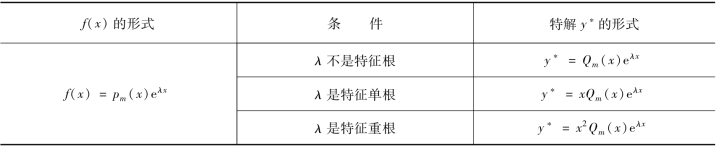
因为方程（5-31）右端f（x）是多项式pm（x）与指数函数eλx的乘积，而多项式与指数函数乘积的导数仍然是同一类型的函数，所以从方程（5-31） 的结构可以推断出它应该有多项式与指数函数乘积型的特解，且特解形式如表5-2 所示（其中Qm（x）是与pm（x）同次的多项式）.

表5-2

【例4】 求微分方程y″-2y′=3x+1 的特解.

解 pm（x） =3x+1是一个一次多项式，属于pm（x）eλx型.因为方程内不含y项，而有y′项，所以要使方程两边相等，特解应比右边多项式高一次.

【例5】 求微分方程y″-2y′+4y=4e2x的通解.

解 原微分方程对应的齐次方程的特征方程为

特征根为

所以，对应的线性齐次方程的通解为

又因为λ=2 不是特征方程的根，故设 y*=be2x

把y*，y*′，y*″代入原方程，得

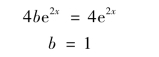
所以，得

从而，原方程的通解为

（2） f（x） =pm（x）eαxcosβx（或pm（x）eαxsinβx）.其中α，β是常数，pm（x）是m次多项式.

这种形式的方程的一般形式为

其中α，β为实数，pm（x）为m次多项式.

由于pm（x）eαxcosβx与pm（x）eαxsinβx分别是pm（x）e（α+iβ）x的实部与虚部根据定理5，方程

的解的实部与虚部分别是方程（5-32）和方程（5-33）的解.

因此，求方程（5-32）或方程（5-33）的通解步骤为：

1）求对应的齐次方程的通解Y=C1y1+C2y2.

2）按自由项f（x） =pm（x）eλx的解法，求方程y″+py′+qy=pm（x）e（α+iβ）x的一个特解y*.

3） y*的实部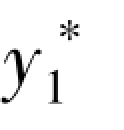是方程（5-32）的解，y*的虚部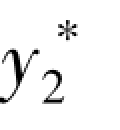是方程（5-33）的解.(www.xing528.com)

4）方程（5-32）的通解为y=Y+方程（5-33）的通解为y=Y+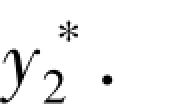

【例6】 求微分方程y″+3y=sin2x的特解.

解 原方程的特解设为y=Asin2x，代入原方程，得

得

所以原方程的特解是y=-sin2x.

【例7】 求微分方程y″+y′-2y=excosx的通解.

解 所求方程对应的齐次方程y″+y′-2y=0 的特征方程为

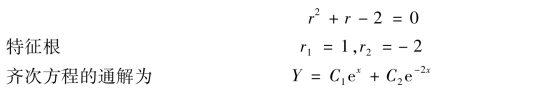
因为1 ±i不是特征根，故设所求方程的特解为

将y*，y*′，y*″代入原方程，得A=2，所以，原方程的通解为

练 习5-3

求下列微分方程的通解或满足初始条件的特解.

习 题5-3

1.判断下列函数组的线性相关性.

（1） x，x2；（2） sin2x，sinxcosx；（3） e2x，e3x.

（4） exsin2x，e2xsinx；（5） arctanx，5arctanx；（6） xlnx，xln2x.

2.求下列方程的通解.

（1） y″+5y′+6y=0；（2） y″+8y′+16y=0；（3） y″-4y′+13y=0；

（4） y″+2y′+5y=0；（5） y″-y′-30y=0；（6） y″-6y′+9y=0.

3.求下列方程满足初始条件的特解.

（1） y″-4y′+3y=0，y|x=0=6，y′|x=0=10；

（2） y″-2y′+y=0，y|x=0=4，y′|x=0=2.

4.求下列微分方程的通解.

（1） y″+y′=x2； （2） y″-3y′+2y=xe2x；

（3） y″+6y′+5y=e2x；（4） y″-2y′+y=4xex；

（5） y″+2y′+5y=5x+2；（6） y″-2y′+5y=exsin2x；

（7） y″-2y′+3y=e-xcosx；（8） y″-7y′+6y=sinx.

5.求下列方程满足初始条件的特解.

（1） y″-3y′+2y=5，y|x=0=1，y′|x=0=2；

（2） y″-y=4xex，y|x=0=0，y′|x=0=1；

（3） y″+y=2xex+4sinx，y|x=0=0，y′|x=0=0.