实用微积分：一阶线性微分方程的求解

可化为形如

称为对应于方程（5-17）的二阶线性齐次微分方程.

方程（5-18）是可分离变量的，分离变量后，得

两边积分，得

于是，方程（5-18）的通解为

现在来分析一阶线性非齐次方程（5-17）的通解.把方程（5-17）改写为

两边积分，得

上式右端第一项是对应的线性齐次方程（5-18） 的通解，第二项是线性非齐次方程（5-17）的一个特解（即在通解（5-21）中令C=0，便得此特解），因此，一阶线性非齐次方程的通解等于对应的线性齐次方程的通解与线性非齐次方程的一个特解之和.

【例6】 求解微分方程y′-ycotx=2xsinx.

解法一 常数变易法

对应齐次方程为

分离变量，得

两边积分，得

用常数变易法，把C换成新的未知数C（x），

即令

代入原非齐次方程，得

两边积分，得

故所求通解为

解法二 公式法

故

【例7】 减肥的问题实际上是减少体重的问题，假定某人每天的饮食可产生AJ热量，用于基本新陈代谢每天所消耗的热量为BJ，用于锻炼所消耗的热量为CJ/（d·kg）.为简单计，假定增加（或减少）体重所需热量全由脂肪提供，脂肪的含热量为DJ/kg，求此人体重随时间的变化规律.(www.xing528.com)

解 建立微分方程和定解条件，设t时刻（单位： d） 的体重为w（t），根据热平衡原理，在dt时间内，

即

记

则得方程

设开始减肥时刻为t=0，体重为w0，于是初始条件为

解微分方程得

代入初始条件可得特解为

由上面的结果易得出如下结论：

（4）可以进一步讨论限时减肥（例如举重运动员参赛前体重要降到规定的数值） 或限时增肥（例如养猪场要在一定时间内使猪的重量达到一定值）问题，这就是要设计出a与b的最佳结合，使体重在限期t=T时达到允许的体重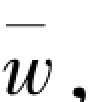即

这个问题较复杂，这里不再详细讨论.

练 习5-2

求下列微分方程的通解：

（1） y′-eysinx=0； （2） xy′=y（1 +lny-lnx）；

（3） （cosx）y′+（sinx）y=1；（4） y′+2y=4x.

习 题5-2

1.求下列微分方程的通解：

（7） （1 +x2）y′-2xy=（1 + x2）2；（8） y′-3xy=2x；（9） y′=（x-y）2+1；

（10） y′cosx+ysinx=cos2x.

2.求下列微分方程满足初始条件的特解.