定积分在几何中的实用应用

1.平面图形的面积

一般地，求由区间[a，b]上的连续曲线y=f（x），y=g（x）（g（x） ≤f（x））以及直线x=a、直线x=b围成的平面图形的面积如图4-12 所示，用微元法分析如下：

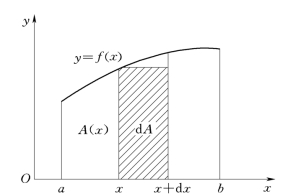
图4-11

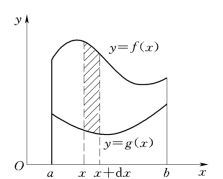
图4-12

（1）任意一个小区间[x，x+dx] （其中，x、x+dx∈[a，b]）上的窄条面积dS可以用底为dx，高度为f（x） -g（x）的窄条矩形的面积来近似计算，即面积微元为

（2）以[ f（x） -g（x）]dx为被积表达式，在区间[a，b]上积分，得该平面图形的面积

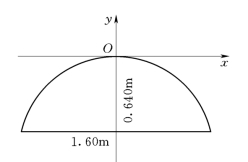
图4-13

所以窗户的面积为0.683m2.

【例2】 一个工程师正用CAD设计一游泳池，游泳池的表面是由曲线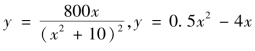以及x=8 围成的图形，如图4-14 所示，求此游泳池的表面面积.

解 解联立方程组

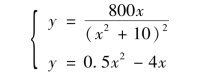
得两条曲线的左交点为（0，0），右交点的横坐标大于8，于是，面积微元为

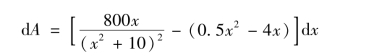
此游泳池的表面面积为

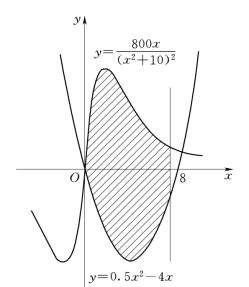
图4-14

解 椭圆关于两坐标轴都对称，所以椭圆所围成图形的面积为A=4A1，A1为该椭圆在第一象限与两坐标轴所围图形的面积（图4-15），因此

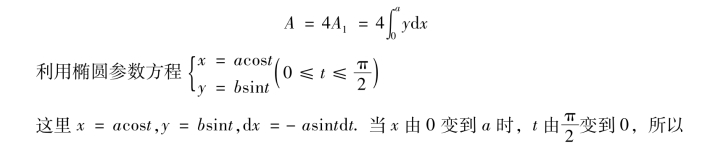
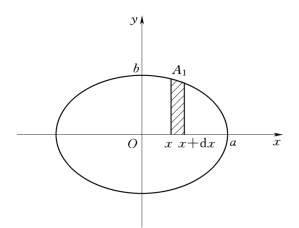
图4-15

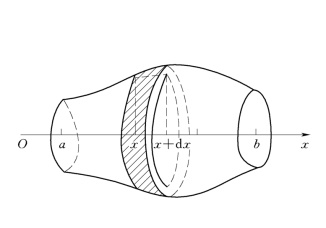
图4-16

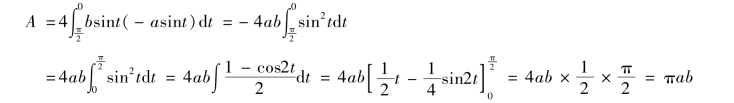
当a=b时，就得到圆面积的公式A=πa2.

2.立体的体积

（1） 平行截面面积为已知的立体的体积.设有一立体，如图4-16 所示，在分别过直线x=a，x=b且垂直于x轴的两平面之间，它被垂直于x轴的平面所截的截面面积为已知的连续函数A（x），这种立体的体积可以用定积分来计算.

取x为积分变量，积分区间为[a，b]，在[a，b] 上取代表区间[x，x+dx]，相应薄片的体积近似于底面积为A（x），高为dx的柱体体积，即体积微元

从而，所求立体的体积

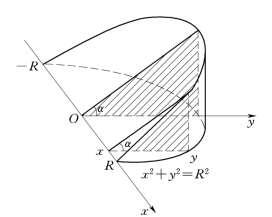
图4-17

(www.xing528.com)

图4-18

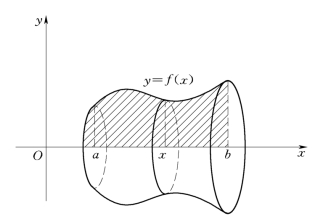
【例4】 一平面经过半径为R的圆柱体的底圆中心，并与底面夹角为α，截得一楔形立体（图4-17），求这楔形立体的体积.

解 取这个平面与圆柱体的底面交线为x轴，底面上过圆心且垂直于x轴的直线为y轴，那么底圆的方程为x2+y2=R2，过x轴上的点x且垂直于x轴的平面截立体所得的截面是直角三角形，它的两条直角边的长度分别为y及ytanα，因此截面面积为

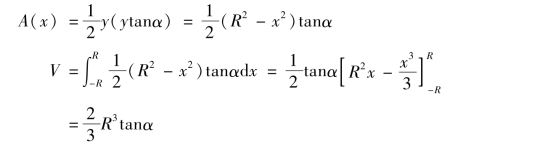
（2） 旋转体的体积.旋转体是由平面内的一个图形绕该平面内的一条定直线旋转一周而成的立体，这条定直线称为旋转体的轴.

设一旋转体是由连续曲线y=f（x），直线x=a，直线x=b及x轴围成的曲边梯形绕x轴旋转一周而成（图4-18），现计算它的体积.

取横坐标x为积分变量，积分区间为[a，b]，用过点x，x∈[a，b]且垂直于x轴的平面截旋转体，所得的截面是半径为|f（x） |的圆，则截面面积为

A（x） =π|f（x） |2=π[f（x）]2得体积微元

于是旋转体的体积

同理，由连续曲线x=φ（y）与直线y=c，直线y=d及y轴围成的曲边梯形绕y轴旋转而成的旋转体的体积（图4-19）

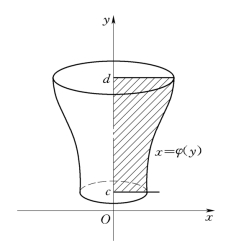
图4-19

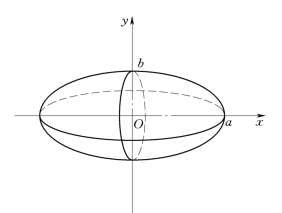
图4-20

当a=b，便得到半径为a的球体的体积

【例6】 某人正在用计算机设计一台机器的底座，它在第一象限的图形由y=8 -x3、y=2 以及x轴、 y轴围成，底座由此图绕y轴旋转一周而成，如图4-21 所示，试求此底座的体积.

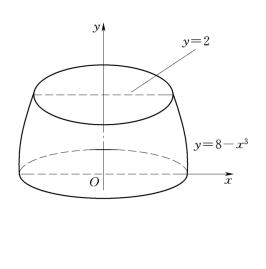
图4-21

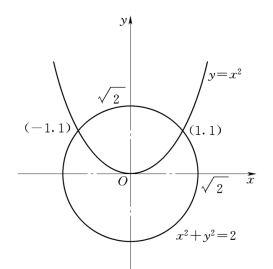
图4-22

而所求体积为

3.平面曲线的弧长

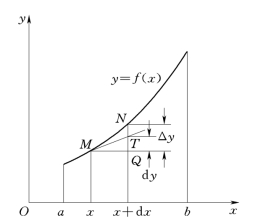
图4-23

这一函数称为悬链线，它表示的是一悬挂在空中的线缆的形状，求此悬链线x=-1和x=1 之间的长度.

解

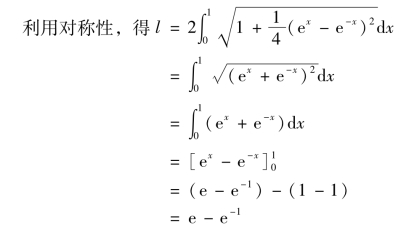
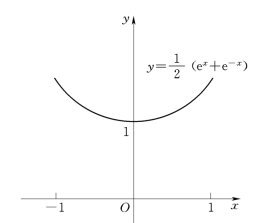
图4-24