如何保证函数的原函数存在

前面我们给出了原函数的定义，关于原函数这里要说明三点：一是原函数的存在性；二是原函数的个数；三是原函数间的关系.

第一，一个函数具备什么条件才能保证它的原函数一定存在？这里给出一个结论.

定理2 （原函数存在定理） 如果函数f（x）在区间I上连续，那么在区间I上存在可导函数F（x），使得对任意x∈I，都有F′（x） =f（x）.

简单说就是：连续函数一定有原函数.由于初等函数在其定义域内都是连续的，所以，初等函数在其定义域区间内都有原函数.

第二，如果函数f（x）在区间I上有原函数，那么它的原函数是不是唯一的？

设F（x）是f（x）在区间I上的一个原函数，即F′（x） =f（x），x∈I，显然，对于任何常数C，也有

即对任何常数C，F（x） +C也是f（x）的原函数，这说明，如果f（x）有一个原函数，那么f（x）就有无限多个原函数.

第三，如果F（x）是f（x）在区间I上的一个原函数，那么f（x）的其他原函数与F（x）有什么关系？

设φ（x）是f（x）的另一个原函数，即当x∈I，有

于是，[φ（x） -F（x）]′=φ′（x） -F′（x） =f（x） -f（x） =0.

在上一章中已经知道，在一个区间上导数恒为零的函数必为常数.所以，φ（x） -F（x） =C（C为某个常数）.

这表明φ（x）与F（x）只差一个常数，因此，当C为任意常数时，表达式

就可表示f（x）的全体原函数（称为原函数族）.(www.xing528.com)

有了以上关于原函数族的概念，我们就可以引入不定积分的定义.

定义 设函数F（x）是f（x）在区间I上的一个原函数，则函数f（x）的全体原函数称为函数f（x）在区间I上的不定积分，记为∫f（x）dx，即

其中，记号∫称积分号，f（x）称被积函数，f（x）dx称被积表达式，x称积分变量，C称积分常数.

按照定义，要计算函数的不定积分，只需求出它的一个原函数，再加上任意常数C即可.

从不定积分的概念可以知道，“求不定积分” 和“求导数” 或“求微分” 互为逆运算，即有

反之，则有∫F′（x）dx=F（x） +C 或 ∫dF（x） =F（x） +C.

这就是说，若先积分后微分，则两者的作用相互抵消；反过来，若先微分后积分，则应该在抵消后加上任意常数C.

注意：由于不定积分是被积函数的全体原函数，所以在求出被积函数的一个原函数之后，不要忘记加积分常数C.

通常我们把一个原函数F（x）的图像称为f（x）的一条积分曲线，其方程为y=F（x），因此，不定积分∫f（x）dx在几何上就表示全体积分曲线所组成的曲线族，它们的方程是y=F（x） +C.

在几何上，规定：如果两条曲线在横坐标相同点处具有相同的切线斜率，则称这两条曲线平行.这样，不定积分在几何上就表示一族彼此平行的曲线（图4-6）.

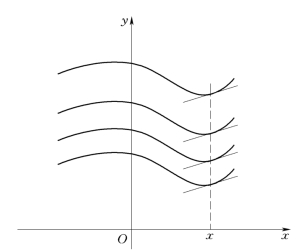
图4-6