在第一章绪论中,已经介绍了变速直线运动的瞬时速度问题.当时间的改变量Δt很小时,变速直线运动可以近似地看成匀速直线运动,从t0到t0+Δt的时间段内物体的平均速度为
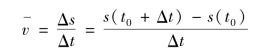
就是物体在t0时刻瞬时速度υ(t0)的近似值,Δt越小,这个近似值就越精确,从而将求变速直线运动物体的瞬时速度归结为求平均速度的极限,即
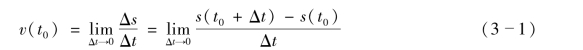
还有许多实际问题都可归结为求同样形式的极限,下面举一例.
【例1】 平面曲线的切线斜率问题.
在很多实际问题中都提出求曲线的切线斜率问题,怎样定义曲线在一点处的切线呢?
在中学几何里,圆的切线被定义为“与圆只有一个交点的直线,”但对一般曲线而言,就不能用与曲线只有一个交点的直线作为切线的定义,那么,一般曲线的切线又怎样定义呢?
如图3-1 所示,设y=f(x)在(a,b) 内连续,x0为(a,b)内一点,求曲线上点M(x0,y0)处的切线斜率.
在曲线y=f(x)上取点M(x0,y0)附近一点M1(x0+Δx,y0+Δy),作割线MM1,它的倾角为φ,则
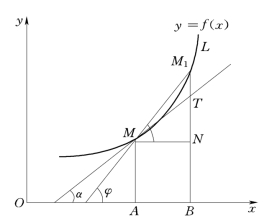
图3-1
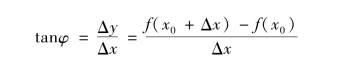
就是割线MM1的斜率,当Δx→0 时,点M1就沿着曲线趋向点M,割线MM1将绕着点M转动,如果它的极限位置存在,设为MT,那么MT就称为曲线y=f(x)在点M处的切线.
因此,当Δx→0 时,割线MM1就转化成切线MT,割线的斜率就转化为曲线在点M处切线的斜率
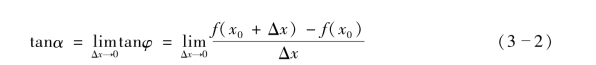
上述对于变速直线运动的速度和平面曲线的切线斜率问题,尽管它们的意义各不相同,但从数学结构上看,其实质是相同的,都可归结为计算函数增量与自变量增量的比值当自变量增量趋于零时的极限,由此可以得到函数在某一点处导数的定义.

显然,对于可导函数f(x)而言,f(x)在点x0处的导数f′(x0),就是它的导函数f′(x)在点x=x0处的函数值,即


有了导数的定义,前面变速直线运动的速度和平面曲线切线的斜率就可分别叙述为:(https://www.xing528.com)
作变速直线运动的物体在时刻t0的瞬时速度就是位置函数s=s(t)在t0的导数,即
![]()
曲线y=f(x)在点M(x0,y0)处切线的斜率就是函数y=f(x)在点x0处的导数,即
![]()
由导数的定义可知,求函数y=f(x)的导数可以分为三个步骤:
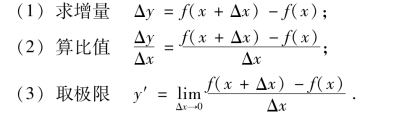
下面,根据这三个步骤举两个简单的例子.
【例2】 求下列函数的导数.
(1) y=C(C∈R);(2) y=x.
解 (1)函数y=C是常函数,即不论自变量x取何值,函数值都是常数C,由于在任意点x处的导数就是该点函数的变化率,显然常函数的导数应等于零,用三个步骤可得同样结论.
求增量 Δy=C-C=0 ;

(2)函数y=x,表达了自变量x的取值恰好就是相应的函数值,那么函数相对自变量的变化率应该是1,用三个步骤可得同样结论.
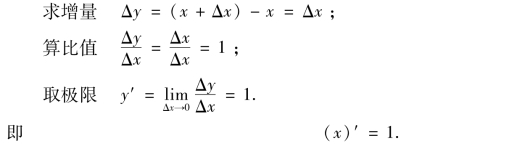
【例3】 求函数y=sinx的导数.
解 给自变量x以增量Δx.
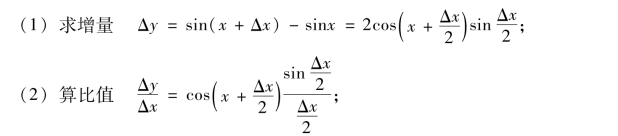
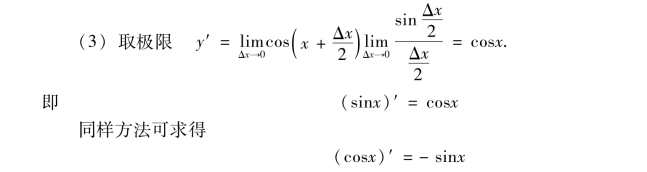
利用导数的定义我们可以推得以下基本初等函数的导数.
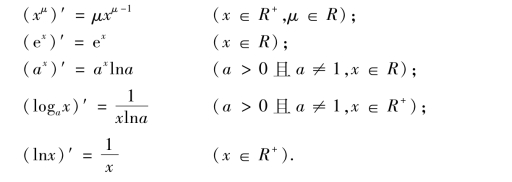
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




