实用微积分：闭区间连续函数性质！

1.最大值和最小值性质

定理4 （最值定理） 闭区间上的连续函数必能取得最大值和最小值.

该定理从几何直观上看是明显的.闭区间上连续函数的图象是包括两端点的一条连续不间断的曲线（图2-25），该曲线上的最高点P和最低点Q的纵坐标分别是函数在闭区间[a，b]上的最大值和最小值.

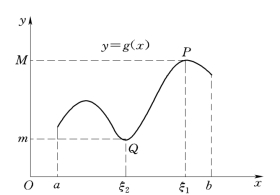
图2-25

图2-26

该定理中的“闭区间”和“连续”的条件不具备时，结论可能不成立.如函数y=x在开区间（0，1）内连续，但它在（0，1）内既无最大值也无最小值.又如函数f（x） =在闭区间[ -1，1]上不连续，函数f（x）在[ -1，1] 上虽然有最大值1，但是无最小值.

推论（有界定理） 闭区间上的连续函数必有界.

2.介值性质

定理5 （介值定理） 闭区间上的连续函数必能取到介于最大值和最小值之间的一切值（图2-26）.

推论（零值定理） 若函数f（x）在闭区间[a，b] 上连续，且f（a）与f（b）异号（即f（a）·f（b） ＜0），则至少存在一点x0∈（a，b），使得f（x0） =0.

即方程f（x） =0 在开区间（a，b）内至少存在一个实根.

【例10】 证明方程x3-4x2+1 =0 在区间（0，1）内至少有一实根.

证 函数f（x） =x3-4x2+1在闭区间[0，1]上连续，且f（0） =1 ＞0，f（1） =-2 ＜0.

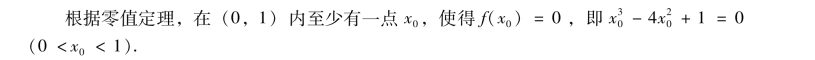
这就说明方程x3-4x2+1 =0 在区间（0，1）内至少有一实根.

练 习2-6

1.选择题.

（1）函数f（x）在点x0处极限存在是f（x）在点x0连续的（ ）.

（A）充分必要条件； （B）必要不充分条件；

（C）充分不必要条件；（D）既不充分也不必要条件.

（2）函数f（x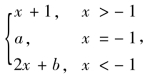） =则f（x）在点x=-1连续的充分必要条件是（ ）.

（A） a=0，b任意；（B） a任意，b=2；

（C） a、 b都任意；（D） a=0，b=2.

2.求下列函数的间断点，并指出间断点的类型.

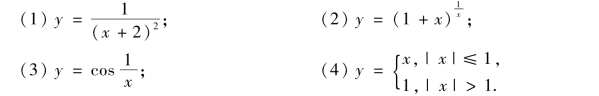(www.xing528.com)

习 题2-6

1.求下列极限：

3.证明方程x3-2x2+3x-1 =0 在区间（0，1）内至少有一实根.

复习检测题二

1.填空题.

2.选择题.

（1）下列函数中是奇函数的是（ ）.

（2）下列函数中，在它的定义域内是单调有界函数的是（ ）.

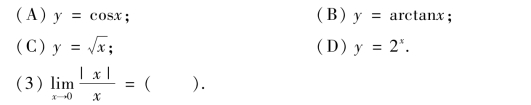
（A） 1；（B） -1；（C） 0；（D）不存在.

（4）当x→0 时，下列函数中与x等阶的无穷小是（ ）.

（5）函数f（x）在点x0有定义是f（x）在点x0有极限的（ ）.

（A）充分必要条件；（B）必要不充分条件；

（C）充分不必要条件；（D）既不充分也不必要条件.

3.求下列极限：

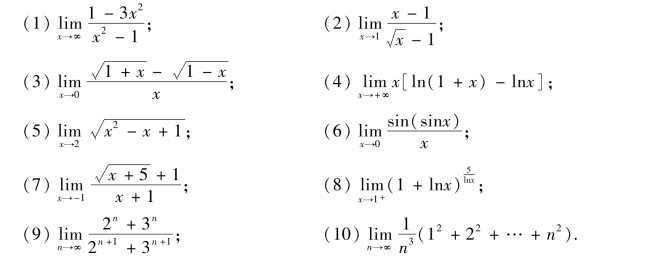
4.设函数

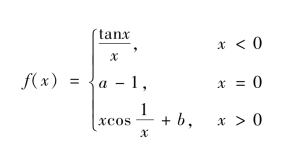
问a为何值时，f（x）在点x=0 左连续？ b为何值时，f（x）在点x=0 连续？

5.证明方程x·2x-1 =0 至少有不小于1 的正根.