函数特性，函数的定义和特点

1.函数的概念

我们知道，圆的面积A和圆的半径r有关，它们之间的关系可表示为A=πr2，即A等于半径r的平方乘以π，可看出面积A随着半径r的变化而变化，此时就说面积A是半径r的函数.下面给出函数的定义.

定义1 设D是非空数集，如果对于变量x在D中的每个取值，按照某个对应法则f，变量y都有唯一确定的值与它对应，则称y是定义在D上的函数，记作

其中x称为自变量，y称为因变量，D称为函数的定义域，数集{f（x） |x∈D} 称为函数的值域.

确定一个函数起决定作用的因素是：定义域D及对应法则f.如果两个函数的定义域相同，对应法则也相同，则这两个函数相同，否则就是不同的两个函数.

函数定义域的确定，通常分以下两种情形.一种是具有实际背景的函数，根据实际背景中变量的实际意义来确定.例如，一物体以速度υ0做匀速直线运动，则物体的位移s与时间t之间的函数关系式是

该函数的定义域就是区间[0，+∞），而不是实数集R.另一种是用抽象的数学式子表示的函数，其定义域是使得该数学式子有意义的一切实数组成的集合.例如，函数的定义域是满足不等式1 -x2≥0 的x形成的集合，即闭区间[ -1，1].

2.函数的表示法

表示函数的方法常用的有三种：表格法、图示法和公式法（解析法）.

（1） 表格法.将自变量的某些取值和与其对应的函数值列成表格表示函数的方法称为表格法.

【例1】 某学校2001 ～2005 年每年的招生数量（人）见表2-1.

表2-1

上表表示了该学校招生数量w与年份t之间的函数关系式.

表格法的优点是直观、精确.

（2） 图示法.用图形表示函数的方法称为图示法.

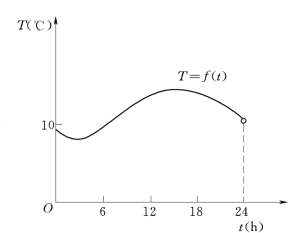
图2-3

【例2】 某地某日的气温T和时间t是两个变量，由气温自动记录仪描得一条曲线（图2-3），这个图形表示了气温T和时间t（从0 时开始）之间的函数关系，记录的时间范围是[0，24） （h）.

图示法的优点是直观、通俗、一目了然.

（3） 公式法.用数学解析式子表示函数的方法称为公式法，又称为解析法.例如，函数y=x2+1，y=2sinx-3 等都是用公式法表示的函数.(www.xing528.com)

公式法的优点是便于数学上的分析和运算.

3.特殊的解析函数

在用公式法表示函数时，常会碰到以下几种特殊情形.

（1）分段函数.在生产实践和科学技术中，常会遇到一个函数在定义域的不同范围内，用不同的解析式表示的情形，如下面两例.

【例3】 在电子技术中遇到的矩形波的函数（图2-4） 在一个周期[ -π，π） 内的解析式为

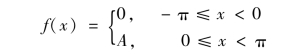
【例4】 符号函数（图2-5）的解析式为

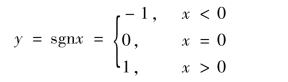
例3、例4 虽然都是用公式法表示的函数，但它们又代表了不同的情形，一个函数要用几个式子表示.像这种在自变量的不同变化范围中，对应法则用不同的式子表示的一个函数，叫做分段函数.

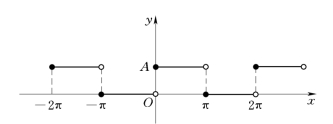
图2-4

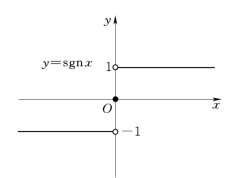
图2-5

注意：分段函数在整个定义域上是一个函数，而不是几个函数；求分段函数值时，应把自变量的值代入相应取值范围的表达式中进行计算；分段函数的定义域是各段自变量取值集合的并集.像例3、例4 所表示的函数都是分段函数，它们的定义域都是实数集R.

（2）隐函数.若变量x、 y之间的函数关系是由一个含有x、 y的方程F（x，y） =0 给出的，则称y是x的隐函数.相应地，把直接由自变量的式子表示的函数y=f（x）称为显函数.如x+y3-1 =0，ex+xy-ey=0等确定的函数都是隐函数.有些隐函数可以化为显函数，例如x+y3-1 =0可以化为这个过程叫做隐函数的显化，但不是每个隐函数都可以显化，如方程ex+xy-ey=0确定的隐函数是无法显化的，因此隐函数是公式法表达函数必不可少的一种形式.

（3）由参数方程确定的函数.若变量x、 y之间的函数关系是通过参数方程

给出的，这样的函数称为由参数方程确定的函数，其中t称为参数.例如，摆线的方程为

4.函数的特性

函数的四个特性在初等数学中已作过详细介绍，在此仅将含义和几何意义简单列出，见表

2-2 （表中D为函数f（x）的定义域）.