实用微积分：微积分研究的两个基本问题解决方案

从微积分的创立，我们看到数学研究的对象是从研究常量到研究变量，从研究规则的几何图形到研究变化着的几何图形，是人类对自然界认识的一个大的飞跃，也是数学发展中的一个转折点.在研究的过程中，不但研究的对象不同，而且研究的思想方法也是很不相同的.初等数学主要采用形式逻辑的方法，静止地、孤立地研究问题，而高等数学则是以运动的、发展变化的观点去研究问题.下面以“速度问题” 和“面积问题” 为例，来看微积分的基本思想方法.

1.变速直线运动的速度

对于匀速直线运动我们在中学已经知道

但在实际问题中，人们往往遇到的是变速直线运动.

问题1：设作变速直线运动的物体的运动方程为s=s（t）.这个方程习惯上叫做位置函数，现在我们来考察该物体在某一时刻t0的瞬时速度.

由于变速直线运动的速度是连续变化的，所以从整个运动过程来看，运动是变速的即非匀速的，不能用上面的公式来计算它在某一时刻t0的瞬时速度，但从局部来看，在一段很短的时间Δt内（图1-1），速度的变化不_大，又可以近似地看作匀速运动，因而当|Δt|很小时，物体在Δt时间段内的平均速度υ可看作是物体在t0时刻的瞬时速度的近似值.

|Δt|时间内的平均速度为

图1-1

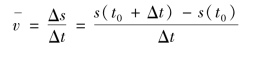
t0时刻的瞬时速度为

|Δt|越小，υ就越接近于t0时刻的瞬时速度υ（t0）.但不论|Δt|多么小，这个平均速度总还是t0时刻瞬时速度的近似值，而不是精确值.

为了从近似值过渡到精确值，我们令Δt→0，当平均速度υ的极限存在时，这个极限值就规定为t0时刻的瞬时速度，即

问题的解决是局部以“匀速”代替“变速”，以平均速度代替瞬时速度，然后通过取极限，达到从瞬时速度的近似值过渡到它的精确值.这一问题的解决方法是微分学的基本概念---导数概念的实例的典型代表.

2.平面图形的面积

中学已学过一些较规则的平面图形的面积计算，但对于由曲线围成的封闭的平面图形的面积计算没有现成的公式可用，下面以求曲边三角形面积为例介绍积分学中解决这类问题的思想方法.

问题2：计算由抛物线y=x2，直线x=1 及x轴围成的平面图形的面积（图1-2，通常称曲边三角形）.(www.xing528.com)

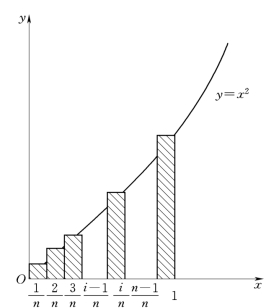
图1-2

显然，该图中由于一边是曲线，不能用三角形或矩形的面积公式来计算.我们遇到的新问题是“曲线与直线” （简称“曲”与“直”）的矛盾.为了解决这一问题，可把区间[0，1] 分成n 等分，再过各分点作y轴的平行线，分整个曲边三角形成许多很窄的（小曲边梯形）竖条，其高度不断变化，但由于它很窄即它的底很短，高度的变化不大，可以把高度在每一个小区间上近似看作不变，即以小矩形的面积来近似代替窄条面积.换句话说，就是在每一个窄条上用“直边”代替“曲边”.这样分割的越细，所得的近似值越接近于精确值.最后通过求和取极限就可得到曲边三角形面积的精确值.

具体做法如下：

把[0，1]区间n等分，那么分点为

每个小区间的长为

相应于每个小区间上小矩形的宽也为，而小矩形的高取成每个小区间的右端点对应的函数值.

第i个小矩形的面积为

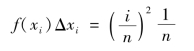
所有小矩形的面积和

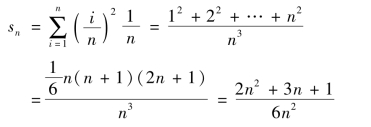
是曲边三角形面积的近似值.

让n无限地增大（记为n→∞），通过取极限，面积的近似值转化为面积的精确值.

这一问题的求解方法是微积分中积分问题的典型代表.积分学中的基本概念---定积分，就是从这类问题中抽象出来的，将在第四章中进行学习.

上述两个例子代表微积分中两类典型问题，具有普遍的意义.从中不难看到，函数是微积分的研究对象，极限是微积分的研究基础和工具，没有极限概念，就无法求得两例中的精确值，只能停留在近似值.有了极限，近似值转化为精确值，才使问题从根本上得以解决.这种求解的思想方法就是微积分思想方法的具体体现.有了这一思想方法，就可以解决一批关于求函数在某点变化率的问题，可以解决一批求函数在某区间变化大小的问题.因此从中不难看出，导数和积分分别是从局部和整体认识同一事物的两个方面.导数是研究函数在一点处的变化情况的，仅与函数在该点附近局部性态有关，而积分则研究函数在一个区间上的变化，与函数在该区间上的整体性态有关.它们的研究方法是类似的，都是采取在“微小局部” “以匀代非”、 “以直代曲”或者说“以不变代变” 求得近似值，通过取极限转化为精确值.这就是微积分解决问题的基本思想方法，它体现了通过矛盾的转化解决矛盾的唯物辩证法，是与初等数学主要根据形式逻辑的推演方法有本质的不同.