Patran2010与Nastran2010有限元分析入门

Patran提供了较为丰富的单元库，从点、线、面到实体，都有相对应的单元形状和不同的拓扑形式，参见图4-1。

下面具体介绍各种单元类型。

点单元（Point）：点单元通过节点来创建，其一般用于动态问题中集中质量的处理。在节点处创建点单元，然后将结构中该点处的集中质量赋予该点单元，这样，集中质量所代表的质量力就施加到了节点上。

梁/杆单元（Beam/Bar）：梁杆单元有2节点、3节点和4节点三种拓扑形式（以“Bar”后跟一个表示节点数的数字表示，如Bar2、Bar3、Bar4，其他形式的单元也类似），对应于线性的几何。从几何表达上讲，梁和杆是没有区别的，都用线来表示，但物理特性上来讲，两者是有区别的，所以，Patran中将梁截面特性的定义放在了Properties部分。对于3节点和4节点的梁/杆单元，各节点将均匀的插入到单元中，以提高单元的表达精度。一般来说，在每种单元的端点或拐角位置，都有节点，以表征和维持单元的基本形状，例如杆单元的两个端点，三角形单元的三个顶点。

三角形单元（Tri）：三角形单元有3节点、4节点、6节点、7节点、9节点和13节点等形式，适用于曲面的网格划分。4节点三角形单元的第4个节点位于三角形的中心；6节点三角形单元的每一条边上有三个节点；7节点三角形单元的的每条边上有三个节点，同时中心位置也有一个节点；9节点三角形单元的每条边上4个节点；而13节点三角形单元的每条边上有4个节点，同时内部有4个节点。

四边形单元（Quad）：相对来说，四边形单元的精确度要高于三角形单元，但其适应能力较差，适合于较规则的曲面。四边形单元有4节点、5节点、8节点、9节点、12节点和16节点等形式，适用于曲面网格的划分。当单元节点多于4个时，其节点分布类似于三角形单元。(www.xing528.com)

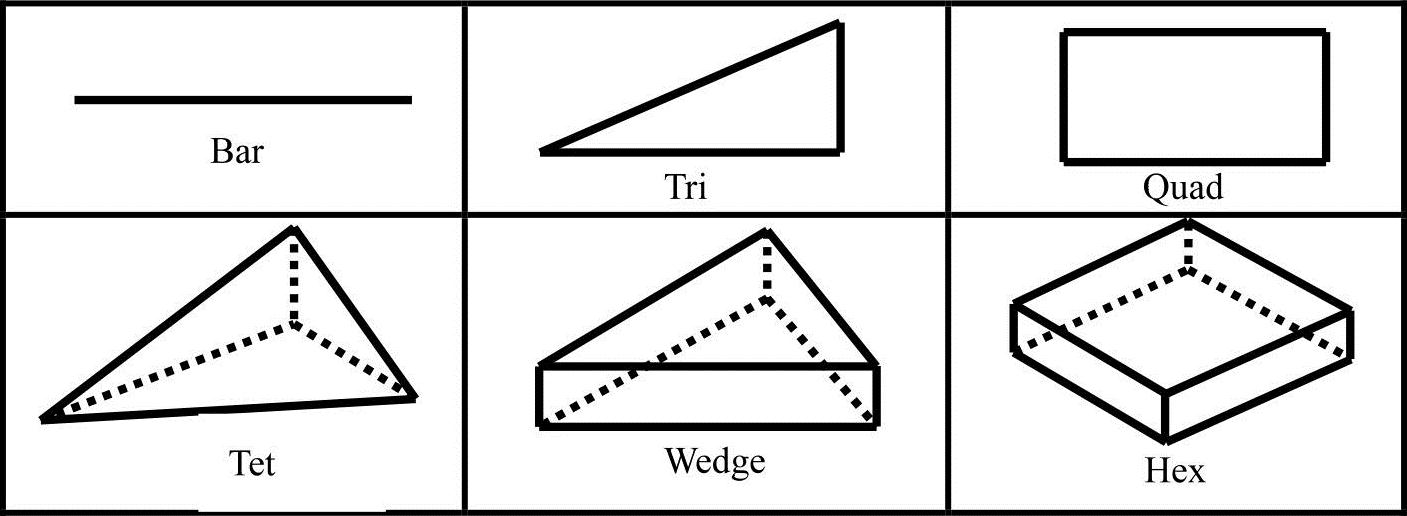
图4-1 Patran中的各种单元形状

四面体单体（Tet）：四面体单元适用于实体网格的划分，其有4节点、5节点、10节点、11节点、14节点、15节点、16节点和40节点等形式。5节点的四面体单元其第5个节点位于四面体的中心部位；10节点的四面体单元其每条边上有3个节点；11节点的四面体单元除了每条边上有3个节点之外，其中心位置也有一个节点；14节点的四面体单元每条边上有3个节点，同时每个面的中心位置也有一个节点；15节点四面体单元的节点分布与14节点的单元类似，只是在单元体的中心位置有个节点；16节点单元的每条边上有4个节点；40节点四面体单元节点的分布比较复杂，其每个面上节点的分布类似于Tri10，单元体的内部有11个节点。

五面体单元（Wedge）：五面体单元也就是楔形单元，其有6节点、7节点、15节点、16节点、20节点、21节点、24节点和52节点等类型。7节点的五面体单元内部有一个节点；15节点的五面体单元每条边上有3个节点；16节点的五面体单元除了每条边上有3个节点之外，内部还有一个节点；20节点五面体单元的节点分布是这样的，在两个三角形表面之间插入一个面，这个面上节点的分布类似于Tri6，而两个三角形表面上节点的分布类似于Tri7；21节点五面体单元节点的分布类似于Wedge20，只是单元中心多了一个节点；52节点五面体单元节点的分布是这样的，在两个三角形表面之间插入两个三角形平面，总共四个三角形平面，每个三角形平面上节点的分布类似于Tri13。

六面体单元（Hex）：六面体单元相对于四面体和五面体单元来说，适用性稍差，但其精度最高，适用于较规则实体的网格划分。六面体单元有8节点、9节点、20节点、21节点、26节点、27节点、32节点和64节点等类型。9节点的六面体单元是在单元体的中心位置有一个节点；20节点的六面体单元是每条边上有3个节点；21节点的六面体单元体比20节点的单元体在中心位置多了一个节点；26节点的六面体单元是每条边上有3个节点，同时每个表面的中心位置还有一个节点；27节点的六面体单元是在单元体中心位置比26节点的单元多了一个节点；32节点的六面体单元是在每条边上有4个节点；64节点的六面体单元是在两个相对四边形表面之间插入两个平面，这样就可得到准平行的4个四边形，这4个四边形平面中节点的分布类似于Quad16。