递归算法(recursion)有时也称为递归方法,是指一个方法直接或间接地调用自己的算法。递归方法会重复调用自身方法,但一次一次地将问题简单化,直到最简单并已存在解答时为止。递归类型有两种,其一是方法调用其自身,就是直接递归;其二是一个方法依次调用另一个方法,被称为间接递归。下面,以递归方法解Hanoi塔问题为例来说明递归方法的应用。
【例4-7】(Hanoi塔问题)设有3根柱子分别记为A,B,C。A柱上有n个带孔的盘子,按规定大盘必须在小盘的下面,如图4-3所示。要求将这n个盘子从A柱借助于B柱移到C柱,每次只允许移动一个盘子,且在移动过程中都必须保持大盘在小盘的下面。求其解。
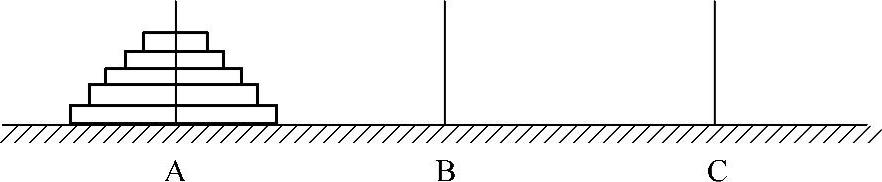
图4-3 Hanoi塔问题示意图


运行结果如下:
在上述程序中,方法hanoi(int n,char one,char two,char three)的定义中两次调用自身方法hanoi(n-1,one,three,two)和hanoi(n-1,two,one,three)。但这两次调用的参数是(n-1),从而保证了递归方法可以归结到n==1的已知解答的情形。称这种已知解答的简单情形为递归基础。通过有限次递归能够归结到递归基础是递归算法有解的必要条件,否则该算法将进入无限次递归的所谓“死循环”状态。
下面以Fibonacci数列F(n)作为第2个递归算法的例题。Fibonacci数列产生于古老的兔子数。关于“兔子数”的有趣故事,可以在任何一本趣味数学书中找到。然而Fibonacci数列在现代计算机密码学、信息隐藏和信号处理等领域中有着重要的应用和研究。(https://www.xing528.com)
【例4-8】(Fibonacci数列)Fibonacci数列F(n),定义如下:
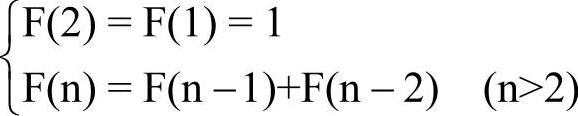
用递归算法编写程序计算F(n)。


运行结果如下:
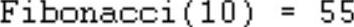
从上述两个例子可以知道,递归方法是一种倒推的方法。要计算第n个结果,就要利用包括第(n−1)个结果在内的以前的结果。因此,递归方法必须有一个基础。比如,对于例4-7 Hanoi塔问题,已知当n=1时其解是A=>C。又如,对于例4-8 Fibonacci数列F(n),已知F(2)=F(1)=1。若没有这样的基础,递归将无结果。注意,递归方法虽然可以使程序简洁,但当递归的深度较大时,即当n较大时,运算效率将降低,甚至会出现“死机”现象。
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




