底物浓度对酶反应速率的影响：生物化学第2版

（一）底物浓度曲线

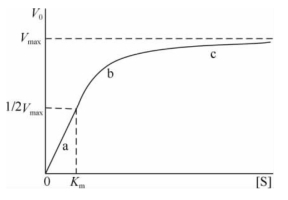
图3-11　底物浓度对酶促反应速率的影响

（a）一级反应　（b）混合级反应　（c）零级反应

酶促反应中，在酶浓度、pH、温度等条件不变的情况下，反应速率与底物浓度的关系呈矩形双曲线（rectangular hyperbola）（图3-11）。在酶促反应起始阶段，反应速率迅速增高呈直线上升，这种反应速率与底物浓度呈正比的反应为一级反应（图3-11中a段）。当底物浓度继续增加，反应体系中酶分子大部分与底物结合时，反应速率的增高则渐渐变缓，即反应的第二阶段为混合级反应（图3-11中b段）。如底物浓度再继续增加，所有的酶分子均被底物饱和，反应速率不再增加，曲线平坦。此时反应速率与底物浓度的增加无关，反应为零级反应（图3-11中c段）。

（二）米氏方程式

几乎所有的酶都有上述被底物饱和的现象，只是不同的酶达到饱和时所需要的底物浓度不同而已。解释酶促反应中底物浓度和反应速率关系的最合理的学说是中间产物学说。该学说认为在酶促反应中酶首先与底物形成酶 底物复合物（ES），即中间产物，然后此中间产物再分解为产物和游离的酶。

1913年Leonor Michaelis和Maud Menten经过大量实验，提出了酶促反应速率与底物浓度关系的数学方程式，即著名的米曼方程式，简称米氏方程式（Michaelis equation）。

方程式中Vmax为最大反应速率（maximum velocity），［S］为底物浓度，Km为米氏常数（Michaelis constant），V0是不同［S］时的反应速率。当［S］很低时（［S］≪Km），分母中的［S］可忽略不计，即反应速率与底物浓度成正比，呈一级反应（图3-11的a段）；当［S］很高时（［S］≫Km），Km可忽略不计，此时V0接近Vmax；反应速率达最大速率，此时再增加［S］，反应速率也不再增加，反应呈零级反应，即曲线的平坦段（图3-11的c段）。米氏方程式的推导以两个假设为前提：①稳态观念，当酶促反应趋于稳态时ES的生成速率与分解速率相等。②酶促反应中［S］大大高于［E］，因此［S］的变化在反应过程可忽略不计。鉴于反应过程中，不断有一部分E与S结合生成ES，故游离酶浓度为总酶浓度［E］中减去生成ES中的酶浓度，即［游离酶］=［E］-［ES］，这样

反应式中k1、k2和k3代表各反应的速率常数。当反应处于稳态时，ES生成速率=ES分解速率，即　k1（［E］-［ES］）·［S］=k2［ES］+k3［ES］

设　

Km为米氏常数，则［E］［S］-［ES］［S］=Km［ES］

由于反应速率

将（5）式代入（6）式：

当［S］很高时，所有E都与S生成ES，反应达最大反应速率，此时［E］=［ES］，即

将（8）式代入（7）式，即得米氏方程式：

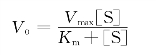
（三）Km和Vmax的意义(www.xing528.com)

（1）当V0=Vmax/2，即反应速率为最大速率一半时，米氏方程为：

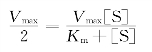
即：Km=［S］

这表示Km等于酶促反应速率为最大反应速率一半时的底物浓度。

（2）已知Km=k2+k3/k1，一些酶的k2≫k3，即ES解离成E和S的速率明显超过分解成E和P的速率，k3可忽略不计，则Km=k2/k1，即此时Km近似ES的解离常数Ks。在这种情况下Km可表示酶对底物的亲和力。

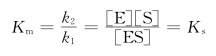
Km愈小，酶和底物亲和力愈大，这表示不需要很高的底物浓度就可达到最大反应速率。但并非所有酶促反应中k3都远小于k2，所以Ks和Km涵义不同。

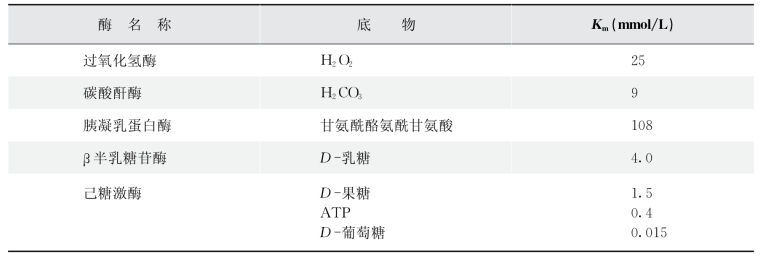
（3）Km是酶的特征性常数，它与酶的结构，酶所催化的底物和反应环境如温度、pH、离子强度等有关，而与酶浓度无关。Km的单位是mol/L，大多数酶的Km值在10-6～10-2mol/L之间，不同种类酶的Km不同（表3-5）；如一种酶有多个不同的底物，则该酶对每一种底物都有其各自特定的Km。

表3-5　某些酶的Km

（4）Vmax是酶被底物完全饱和时的反应速率，当［ES］等于总酶浓度［ET］，即酶被底物完全饱和时：Vmax=k3［ET］

如果知道酶的总浓度和Vmax，即可计算出酶的转换数（turnover number）。当酶被底物完全饱和时，单位时间内每个酶分子（或活性中心）催化底物转变成产物的分子数。

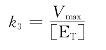
k3即为该酶的转换数，大多数酶的转换数为1～104/s。

（四）Km和Vmax的测定

从图3-11中可知，由于底物浓度对反应速率影响呈矩形双曲线，难以从该曲线中准确测得Vmax和Km。如将米氏方程两侧取倒数处理，得到下面方程式：

以1/V0对1/［S］作图，可得一直线图（图3-12）。此作图法称双倒数作图法或林-贝（Lineweaver-Burk）作图法。从此图可见，直线在横轴上截距为-1/Km，纵轴上截距为1/Vmax，由此直线可较容易地求得Vmax和Km。

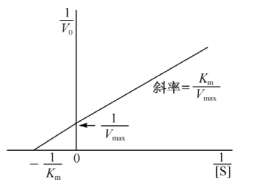
图3-12　双倒数作图法

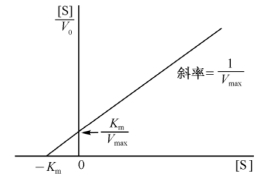
图3-13　Hanes作图法

此外，在上述双倒数方程式两边同时乘以［S］，得下式：

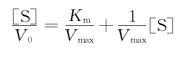
以［S］/V对［S］作图称为Hanes作图法（图3-13），其横轴截距为-Km，直线斜率为1/Vmax。