总成本、收入和利润函数

1.总成本函数

在生产和产品的经营活动中需要有场地、机器设备、劳动力、原材料等投入，称为生产成本.它与商品的产量或销售量q有密切的关系，称为总成本函数，记作C（q）.总成本函数由固定成本C1和可变成本C2（q）两部分组成，即C（q）＝C1＋C2（q），固定成本C1与产量q无关，如场地、设备等；可变成本C2（q）随产量q的增加而增加，如原材料等.

一般情况下，总成本函数是一个增函数，常见的总成本函数有线性函数、二次函数、三次函数等.

评价企业生产的好坏，有时需要用到平均成本这个概念，即生产q个单位产品时，单位产品的成本，记作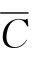，即

例4　生产某种商品的总成本（单位：元）是C（q）＝200＋2q，求生产40件这种商品时的总成本和平均成本.

解

生产40件该商品时的总成本为

C（40）＝200＋2×40＝280（元）

平均成本为

2.收入函数和利润函数

人们总希望尽可能减少成本，提高收入和利润，而收入和利润这些经济变量也都与产品的产量或销售量q密切相关，它们可以看做q的函数，分别称为收入函数和利润函数，记作R（q）和L（q）.

收入可分为总收入R（q）和平均收入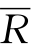.设p为商品价格，q为商品销售量，则有

其中：p（q）是商品的价格函数.

生产一定数量产品的总收入与总成本之差就是其总利润L，即

L＝L（q）＝R（q）-C（q）

它的平均利润为

一般情况下，收入随销售量的增加而增加，而利润并不总是如此，利润函数通常有以下三种情形：

（1）L（q）＝R（q）-C（q）＞0，此时称为有盈余生产，生产利润为正；

（2）L（q）＝R（q）-C（q）＜0，此时称为亏损生产，生产利润为负；(www.xing528.com)

（3）L（q）＝0，此时称为无盈亏生产，把无盈亏生产时的产量记为q0，称为无盈亏点.

例5　设某商品的价格函数是p（q）＝60-0.5q，求该商品的收入函数，并求销售20件商品时的总收入和平均收入.

解

收入函数为

R（q）＝p（q）·q＝60q-0.5q2

平均收入为

由此可得销售20件商品时的总收入和平均收入分别为

例6　已知某商品的成本函数为C（q）＝5＋4q＋q2，若销售单价为10元／件.

求：（1）该商品销售的无盈亏点；

（2）若每天销售10件该商品，为了不亏本，销售单价应定为多少才合适？

解

（1）利润函数为

L（q）＝R（q）-C（q）

＝10q-（5＋4q＋q2）

＝6q-5-q2

由L（q）＝0，即6q-5-q2＝0，解得两个无盈亏点q1＝1和q2＝5.显然，当q＜1或q＞5时，经营亏损；当1＜q＜5时，经营盈利，因此q＝1和q＝5分别是盈利的最低和最高产量.

（2）设销售单价为p元／件，则利润函数为L（q）＝R（q）-C（q）＝pq-（5＋4q＋q2），为使经营不亏本，必须L（10）≥0，即10p-145≥0，也就是p≥14.5.所以，为了不亏本，销售单价应不低于14.5元／件.