闭区间上连续函数的性质简析

闭区间上的连续函数具有一些重要的性质，这些性质有助于我们进一步分析函数.下面介绍几个闭区间上连续函数的基本性质，但略去其严格证明，只借助图像直观地来理解.

定理1.14（最值定理） 在闭区间上连续的函数一定有最大值和最小值.

定理表明：若函数f（x）在闭区间[a，b]上连续，则至少存在一点ξ1∈[a，b]，使f（ξ1）是f（x）在闭区间[a，b]上的最大值，即对任意x ∈[a，b]，有f（x）≤f（ξ1）；又至少存在一点ξ2∈[a，b]，使f（ξ2）是f（x）在闭区间[a，b]上的最小值，即对任意x ∈[a，b]，有f（x）≥f（ξ2）（图1-5）.

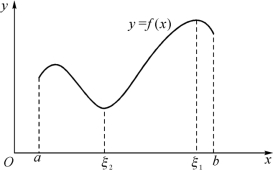
图1-5

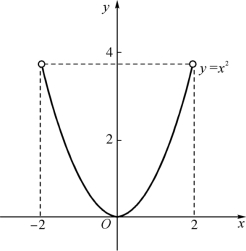
图1-6

如果函数在开区间连续或闭区间上有间断点，那么函数在该区间上不一定有最大值和最小值.例如，函数y=x2在（-2，2）内连续，有最小值但无最大值（图1-6）；又如函数在闭区间[-1，1]上有间断点x=0，它在该区间内也不存在最大值（图1-7）.

注 这两个条件只是最值的充分而非必要条件.

推论 闭区间上连续的函数一定在该区间上有界.

定理1.15（介值定理） 若函数f（x）在闭区间上连续，且f（a）≠f（b），则对于介于f（a）与f（b）之间的任何一个数μ，至少存在一点c∈（a，b），使得f（c）=μ.

定理表明：连续曲线弧y=f（x）与水平直线y=μ 至少相交一点（图1-8）.(www.xing528.com)

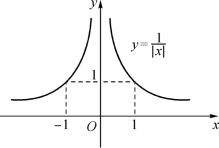
图1-7

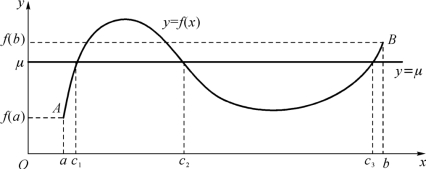
图1-8

推论 在闭区间上连续的函数必取得介于最小值m 和最大值M 之间的任何值.

定理1.16（零点定理） 若函数f（x）在闭区间[a，b]上连续，且f（a）·f（b）＜0，则至少存在一点c∈（a，b），使f（c）=0.

例1.35 证明：方程x5-3x=1在（1，2）内至少有一个实根.

证 设f（x）=x5-3x-1，则f（x）在[1，2]上连续，且由零点定理知，至少存在一点c∈（1，2），使f（c）=0，即方程x5-3x=1在（1，2）内至少有一个实根.

f(1)=-3＜0, f(2)=25＞0.

注 零点定理虽然说明了函数零点的存在性，但没有给出求零点的方法.尽管如此，它仍然具有重要的理论价值.在许多实际问题中，常常会遇到方程求根的问题，如果能预先判定方程在某区间中必有根，就可以用这个定理通过计算机程序算出根的近似值.