VisualBasic程序设计：求最大公约数方法

【例4-25】输入两个正整数，计算并输出它们的最大公约数。

数学方法描述如下。

用大数除以小数，得余数；如果余数等于零，则除数为最大公约数，否则用除数除以余数再次得出一个余数；判断此余数，如果余数等于零，则除数为最大公约数，否则用除数除以余数再次得出一个余数；其余类推，直到余数等于零，那么除数即为最大公约数。

按“三步法”原则分析如下。

做什么

1）用户输入整数两个整数，所以窗体上需要两个文本框。

2）一个“计算”按钮。

怎么做

通过分析不难得出，此问题的特点如下。

1）进行除法运算的次数无法确定，根据用户输入的数据，有可能进行一次除法，就可以计算出最大公约数，但也有可能进行十几次，几十次，或更多次，所以必须考虑用循环结构解决此类问题。并且，循环次数无法确定，不能用For语句来实现，因为For语句适用于预知循环次数的问题，所以这里选择Do…Loop循环结构。

2）根据循环次数的多少，在进行除法运算过程中，可能产生一系列的余数，那么余数的保存方法是解决问题的关键。不能每次都用不同的变量来保存余数，这样就无法循环。因为循环体一旦确定，循环体内的语句、变量也就确定了，循环体的特点就是反复执行相同的语句，循环体内的语句和变量是不能变化的。

通过分析，这里只有3个操作数：被除数、除数、余数，所以用3个变量M、N、R来分别保存被除数、除数、余数。M始终用来保存作为被除数的数据，N始终用来保存作为除数的数据，R始终用来保存刚刚计算出余数。所以这就需要在每次进行除法之前修改变量M、N的值，把被除数存入M，除数存入N，这是循环的关键。例如，当R不等于零时，这时需要用N中的数作为被除数，R中的数作为除数，不能直接用N除以R，而是要执行操作把N中的数传入M中，R中的数传入N中，然后执行M除以N操作，得到余数R，其余类推，这样就可以循环下去了。

步骤描述如下。

1）首先读取用户输入的数据，放入变量M、N中。

2）假设M为较大数，N为较小数，用M除以N，得余数R。

3）如果R等于零，则执行第8）步，否则执行第4）步。

4）把N中的数传入M中。

5）把R中的数传入N中。

6）执行除法M除以N，得到余数R。

7）返回第3）步。

8）输出最大公约数N。

实现

1）上述步骤描述中，循环操作的步骤为第3）～6）步，它们为循环体。(www.xing528.com)

2）对于第3）步的判断，不能用If语句。其实While也是一种判断，若条件满足则进入循环体，若条件不满足则不进入循环体。不是所有的判断都必须用If语句，这要看程序是否有循环，如果需要反复执行相同的某些步骤，则采用循环结构。

实现代码如图4-34所示。

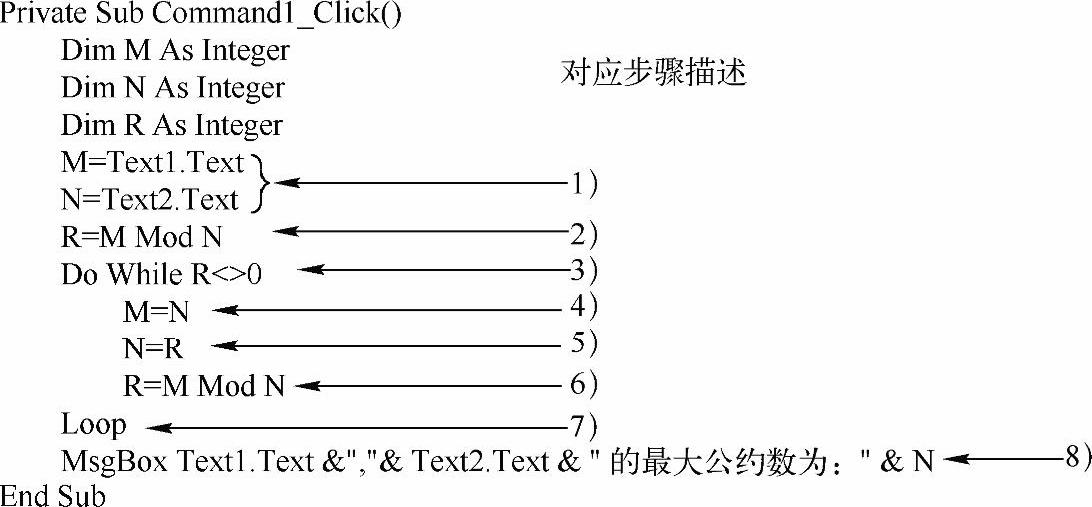
图4-34 求最大公约数

代码中的语句

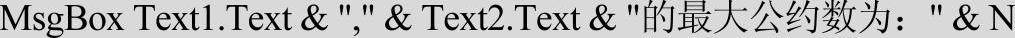
能否改为

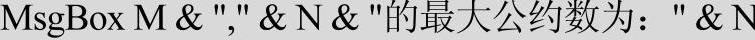
请思考此问题。

采用其他结构的代码如下。

●前测型直到型结构：

●后测型当型结构：

●后测型直到型结构：

●While语句实现。

While与Do…Loop前测型当型结构基本相同，完整代码如下。