裂尖应变场原位实验研究：结果与讨论

图7-3所示为在单轴拉伸载荷下单晶硅中微裂纹的扩展情况，在微裂纹前端可以清晰地看到裂纹尖端。参照图7-3中的两个标记点可以看出微裂纹在连续地向前扩展。以裂纹尖端为坐标原点，将拉伸方向（[100]晶向）作为y轴，将与拉伸方向垂直的方向（[010]晶向）作为x轴建立坐标系。从图7-3中可以看出，随着位移载荷的增加，裂纹主要沿着x轴方向（[010]晶向）扩展（从图7-3a到图7-3b，裂纹向前扩展了66.9μm；从图7-3b到图7-3c，裂纹向前扩展了12.8μm）。

为了分析单晶硅裂纹尖端附近的亚微米尺度应变场，用几何相位分析方法测定裂纹尖端区域（图7-3a和图7-3c中的方框区域，方框区域大小为12.7μm×12.7μm）的应变场。图7-4和图7-5分别给出了图7-3a和图7-3c中方框区域的平面应变场。从图7-4和图7-5中可以看出，变形仅出现在裂纹尖端附近，正应变ε_xx和切应变ε_xy基本为零，应变场主要由正应变分量ε_yy控制，这是因为拉伸方向沿着y轴方向，而且微裂纹是Ⅰ型裂纹。

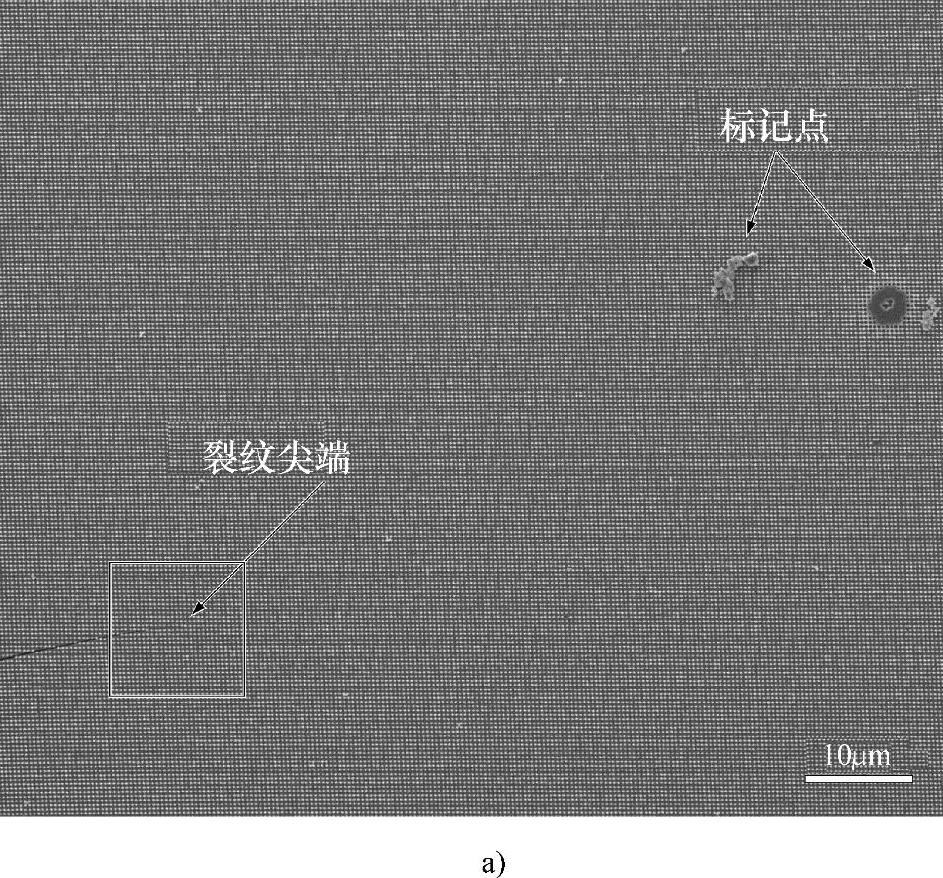
图7-3 单晶硅原位单轴拉伸实验过程中的扫描电子显微镜图像

a）预制裂纹

图7-3 单晶硅原位单轴拉伸实验过程中的扫描电子显微镜图像（续）

b）位移载荷为1.4895μm c）位移载荷为1.6882μm

根据平面应力状态下Ⅰ型裂纹尖端理论应变场公式

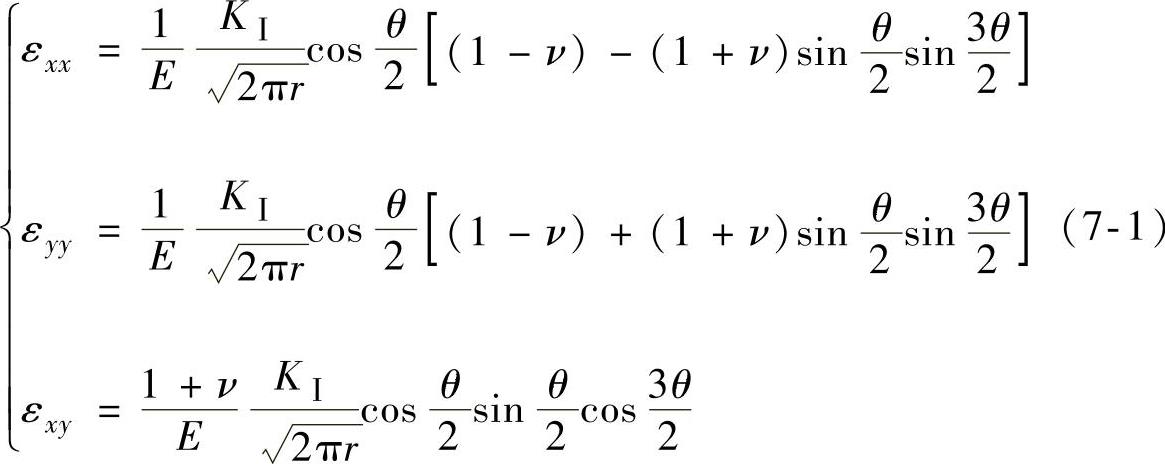
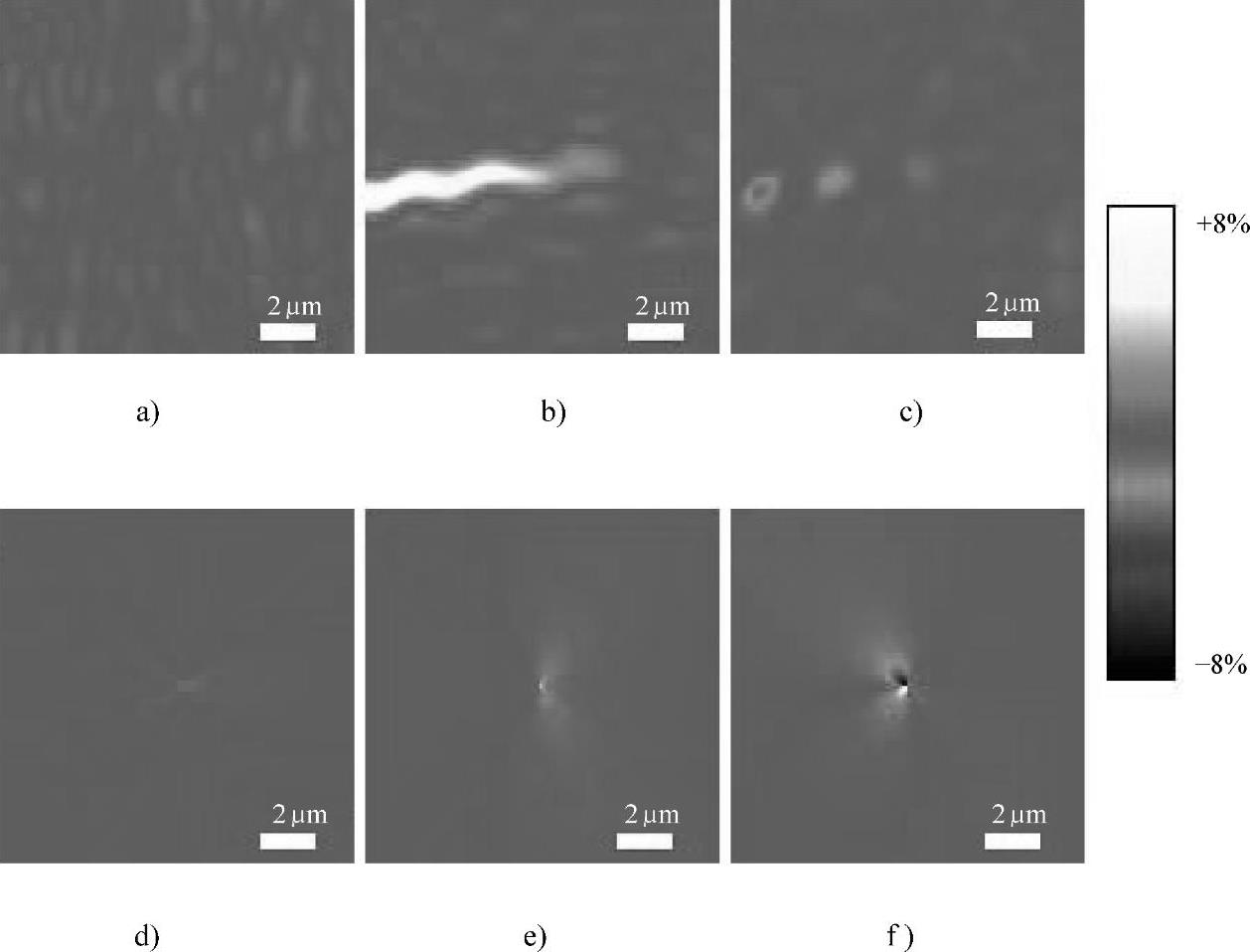
图7-4 图7-3a中方框区域的实验应变场和理论应变场（彩图见文后插页）

a）实验ε_xx应变场 b）实验ε_yy应变场 c）实验ε_xy应变场 d）理论ε_xx应变场 e）理论ε_yy应变场 f）理论ε_xy应变场(www.xing528.com)

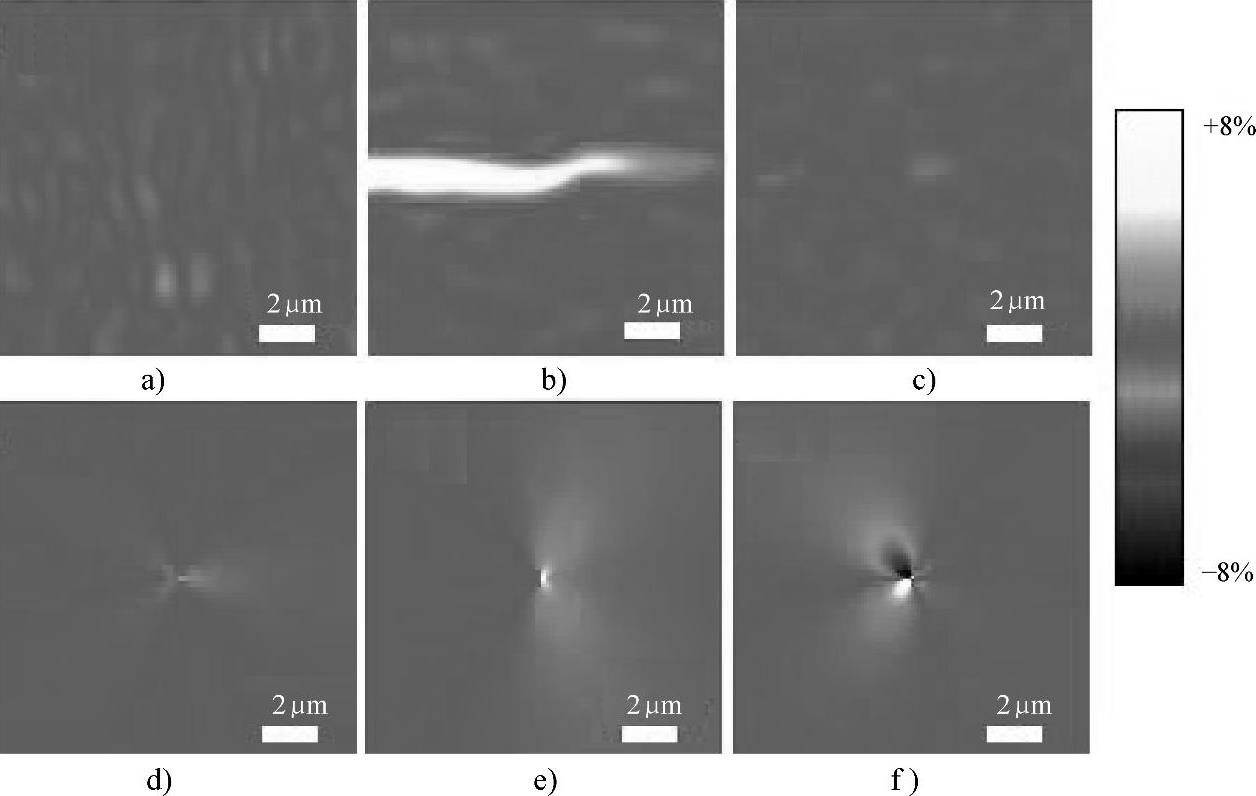
图7-5 图7-3c中方框区域的实验应变场和理论应变场（彩图见文后插页）

a）实验ε_xx应变场 b）实验ε_yy应变场 c）实验ε_xy应变场 d）理论ε_xx应变场 e）理论ε_yy应变场 f）理论ε_xy应变场

可得裂尖前方x轴上的y向应变为

式（7-1）和式（7-2）中E为杨氏模量，ν为泊松比，K_Ⅰ为Ⅰ型裂纹的应力强度因子。

可以利用在远离裂纹尖端区域的实验ε_yy值与理论ε_yy值相等来确定应力强度因子K_Ⅰ的值。因此，在图7-4b中，取x=5.859μm，ε_yy=0.216%，杨氏模量E=107GPa，泊松比ν=0.3，代入式（7-2）可得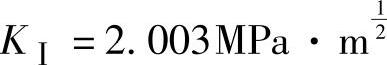，从而可得线弹性理论应变场如图7-4d～f所示。同样地，在图7-5b中，取x=4.121μm，ε_yy=0.663%，杨氏模量E=107GPa，泊松比ν=0.3，代入式（7-2）可得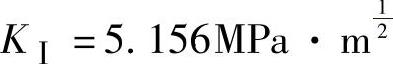，从而可得线弹性理论应变场如图7-5d～f所示。图7-4和图7-5中应变场的变化范围如颜色条所示，最大应变为+8%，对应于白色，最小应变为-8%，对应于黑色，其他应变值介于+8%与-8%之间。可以看出，线弹性理论预测结果与实验应变场差别较大。为了进一步分析裂纹尖端前方的变形情况，从图7-4b、图7-4e、图7-5b和图7-5e提取了裂纹尖端前方且沿着裂纹线方向的实验ε_yy数据和理论ε_yy数据，分别如图7-6和图7-7所示。可以看出，在裂纹尖端前方且沿着裂纹线方向2μm之内，理论值小于实验值。这表明，线弹性断裂力学理论不能描述裂纹尖端区域的变形场，这是因为线弹性断裂力学理论基于连续介质模型，它不适用于亚微米尺度下的裂纹尖端附近区域。在远离裂纹尖端的区域（＞2μm），实验值与理论值符合得很好。此外，从图7-6可以看出，裂纹尖端前方最大应变为3.63%，当位移载荷增加到1.6882μm时，裂纹尖端前方最大应变达到7.08%（见图7-7）。可见，随着位移载荷的增加，裂纹尖端附近的应变也在逐渐增加。

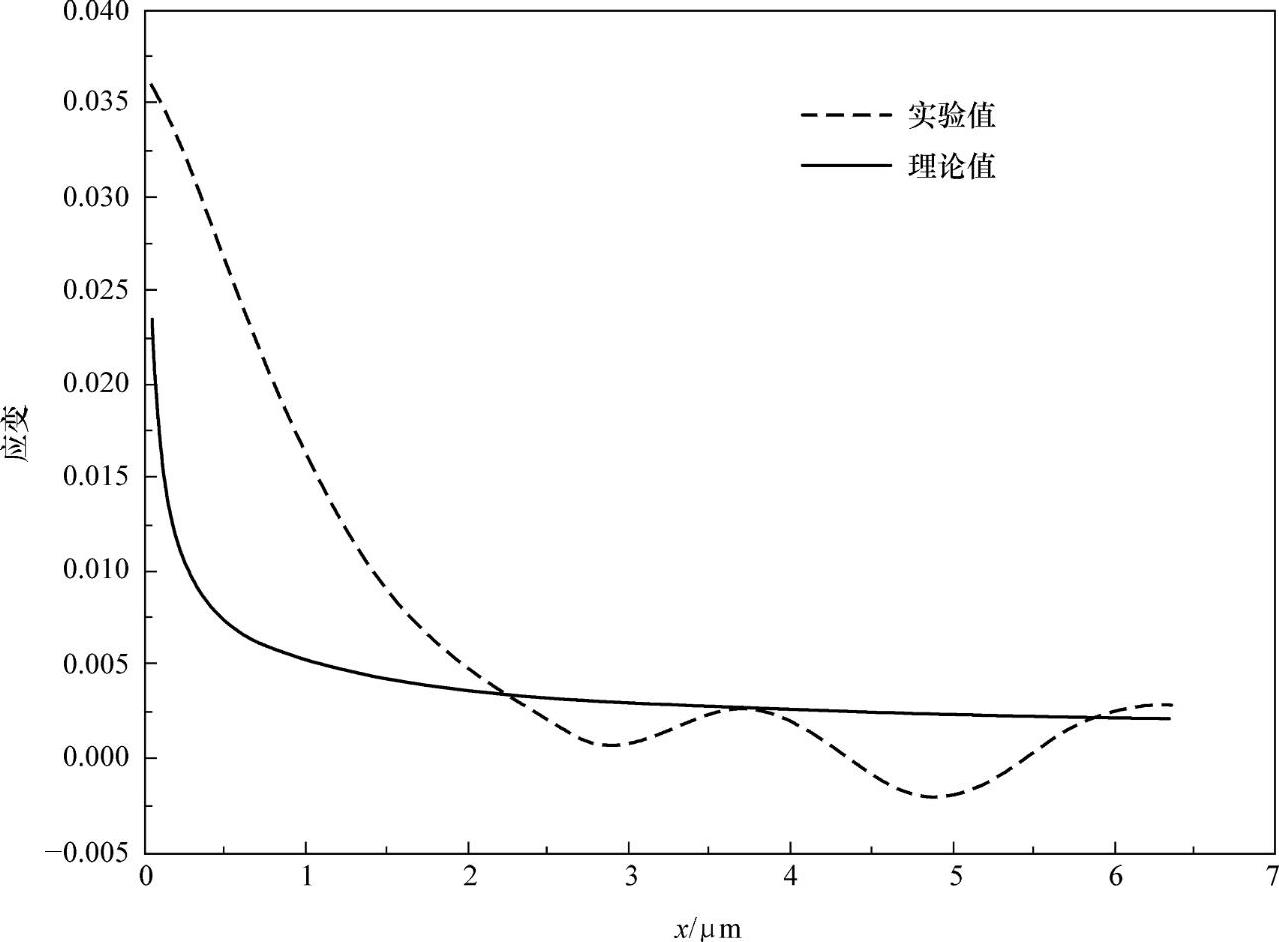
图7-6 图7-3a所示方框区域中裂纹尖端前方且沿着裂纹线方向的实验ε_yy值与理论ε_yy值

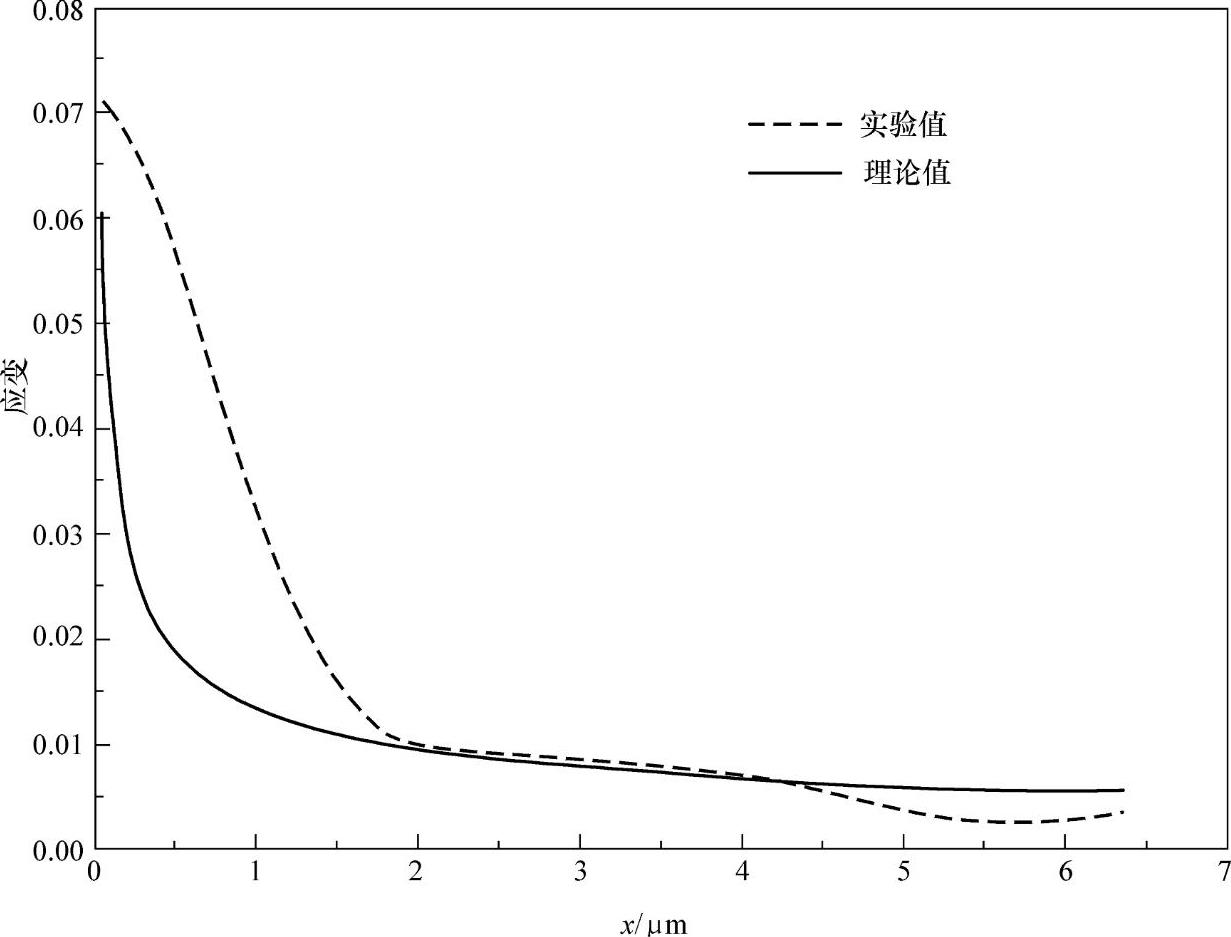
图7-7 图7-3c所示方框区域中裂纹尖端前方且沿着裂纹线方向的实验ε_yy值与理论ε_yy值