微裂纹尖端应变场实验研究

为了进一步分析5A05铝合金中微裂纹的形核及扩展机理，采用几何相位分析方法测定三点弯曲实验过程中缺口及裂纹尖端附近的应变场。

图5-5和图5-6给出了裂纹萌生前缺口附近的平面应变场，其中图5-5所示为载荷上升到150N时（对应于图5-4b）缺口附近的平面应变场，图5-6所示为载荷上升到200N时（对应于图5-4c）缺口附近的平面应变场，应变场的变化范围如颜色条所示，最大应变为+25%，对应于白色，最小应变为-25%，对应于黑色，其他应变值介于+25%与-25%之间。

从图5-5a可以看出，载荷为150N时，正应变ε_yy整体上为零，只有紧靠缺口根部附近有较小的拉伸应变（平均应变为0.91%）。随着载荷的增加，缺口根部附近的正应变ε_yy也逐渐增加（见图5-6a），缺口根部附近在竖直方向处于拉伸状态，但缺口前方大部分区域的正应变ε_yy仍然比较小。从图5-6a可以看到，有两块高应变发射区以与水平方向大约成45°角的方向出现在缺口上下两侧，高应变发射区的平均应变为2.25%，应变图整体上是关于缺口呈对称分布的。

图5-5 用几何相位分析方法测定的载荷上升到150N时（对应于图5-4b）缺口附近的平面应变场（彩图见文后插页）

a）ε_yy应变场 b）ε_xx应变场 c）ε_xy应变场

从图5-5b可以看出，载荷为150N时，正应变ε_xx整体上为零，只有紧靠缺口根部附近有较小的压缩应变（平均应变为-0.96%）。随着载荷的增加，缺口根部附近的正应变ε_xx也逐渐增加（见图5-6b），缺口根部附近在水平方向处于压缩状态，但缺口前方大部分区域的正应变ε_xx仍然比较小。从图5-6b可以看到，有两块高应变发射区以与水平方向大约成45°角的方向出现在缺口上下两侧，高应变发射区的平均应变为-1.63%，应变图整体上是关于缺口呈对称分布的。

图5-6 用几何相位分析方法测定的载荷上升到200N时（对应于图5-4c）缺口附近的平面应变场（彩图见文后插页）

a）ε_yy应变场 b）ε_xx应变场 c）ε_xy应变场

从图5-5c和图5-6c可以看出，切应变ε_xy基本为零，随着载荷的增加，切应变ε_xy的变化不太明显。

图5-7给出了裂纹萌生时（对应于图5-4d）裂纹尖端附近的平面应变场，应变场的变化范围如颜色条所示，最大应变为+25%，对应于白色，最小应变为-25%，对应于黑色，其他应变值介于+25%与-25%之间。图5-7a所示为裂纹萌生时正应变ε_yy的分布，与图5-6a比较可以看出，应变图整体上仍是关于缺口呈对称分布的，两块高应变发射区继续增大（平均应变为3.97%），但该区域的形状和取向基本保持不变。图5-7b所示为裂纹萌生时正应变ε_xx的分布，与图5-6b比较可以看出，应变图整体上仍是关于缺口呈对称分布的，两块高应变发射区继续增大（平均应变为-3.71%），但该区域的形状和取向基本保持不变。图5-7c给出了裂纹萌生时切应变ε_xy的分布，缺口上方有小部分负应变区域，下方有小部分正应变区域，右上方大部分区域为正应变，右下方大部分区域为负应变，应变图整体上基本是关于缺口呈反对称分布的。

对比图5-7a、图5-7b和图5-7c可以看出，正应变ε_yy和ε_xx要比切应变ε_xy大很多，因而应变场主要由正应变ε_yy、ε_xx控制。

图5-8和图5-9所示分别是采用几何相位分析方法测定的最大载荷为420N时（对应于图5-4f）和载荷下降到390N时（对应于图5-4g）裂纹尖端附近的平面应变场，应变场的变化范围如颜色条所示，最大应变为+25%，对应于白色，最小应变为-25%，对应于黑色，其他应变值介于+25%与-25%之间。将图5-8a、图5-9a与图5-7a比较，可以看出，裂纹萌生之后，随着位移的增加及裂纹的扩展，ε_yy应变场的两块高应变发射区迅速增大（图5-8a中高应变发射区的平均应变高达13.66%，图5-9a中高应变发射区的平均应变高达17.25%），但是它们的形状和取向没有改变，仍然是关于缺口呈对称分布的。将图5-8b、图5-9b与图5-7b比较，可以看出，ε_xx应变场与ε_yy应变场有相似的变化规律。将图5-8c、图5-9c与图5-7c比较，可以看出，随着位移的增加及裂纹的扩展，切应变ε_xy也迅速增加，但其仍然基本是关于缺口呈反对称分布的。

将图5-8、图5-9与图5-7比较，可以看出，裂纹萌生之后，随着位移的增加及裂纹的扩展，正应变ε_yy、ε_xx和切应变ε_xy都迅速增加，应变场由正应变ε_yy、ε_xx和切应变ε_xy共同控制，从而导致裂纹扩展的“Z”字形曲折路径。

(www.xing528.com)

图5-7 用几何相位分析方法测定的裂纹萌生时（对应于图5-4d）裂纹尖端附近的平面应变场（彩图见文后插页）

a）ε_yy应变场 b）ε_xx应变场 c）ε_xy应变场

图5-8 用几何相位分析方法测定的最大载荷为420N时（对应于图5-4f）裂纹尖端附近的平面应变场（彩图见文后插页）

a）ε_yy应变场 b）ε_xx应变场 c）ε_xy应变场

需要注意的是，到目前为止，几何相位分析方法主要应用于对高分辨率透射电子显微镜图像的定量分析。本文通过在试样表面制作周期性网格，将几何相位分析方法应用于扫描电子显微镜图像的定量分析。为了验证用几何相位分析方法定量分析扫描电子显微镜图像的可行性，我们同时采用数字图像相关方法对裂纹萌生时（对应于图5-4d）裂纹尖端附近的平面应变场进行了测定，应变场测定结果如图5-10所示。对比图5-7和图5-10，可以看出，几何相位分析方法的测定结果与数字图像相关方法的测定结果基本是一致的，这说明本文采用几何相位分析方法定量分析扫描电子显微镜图像是切实可行的。

图5-9 用几何相位分析方法测定的载荷下降到390N时（对应于图5-4g）裂纹尖端附近的平面应变场（彩图见文后插页）

a）ε_yy应变场 b）ε_xx应变场 c）ε_xy应变场

图5-10 用数字图像相关方法测定的裂纹萌生时（对应于图5-4d）裂纹尖端附近的平面应变场（彩图见文后插页）

a）ε_yy应变场

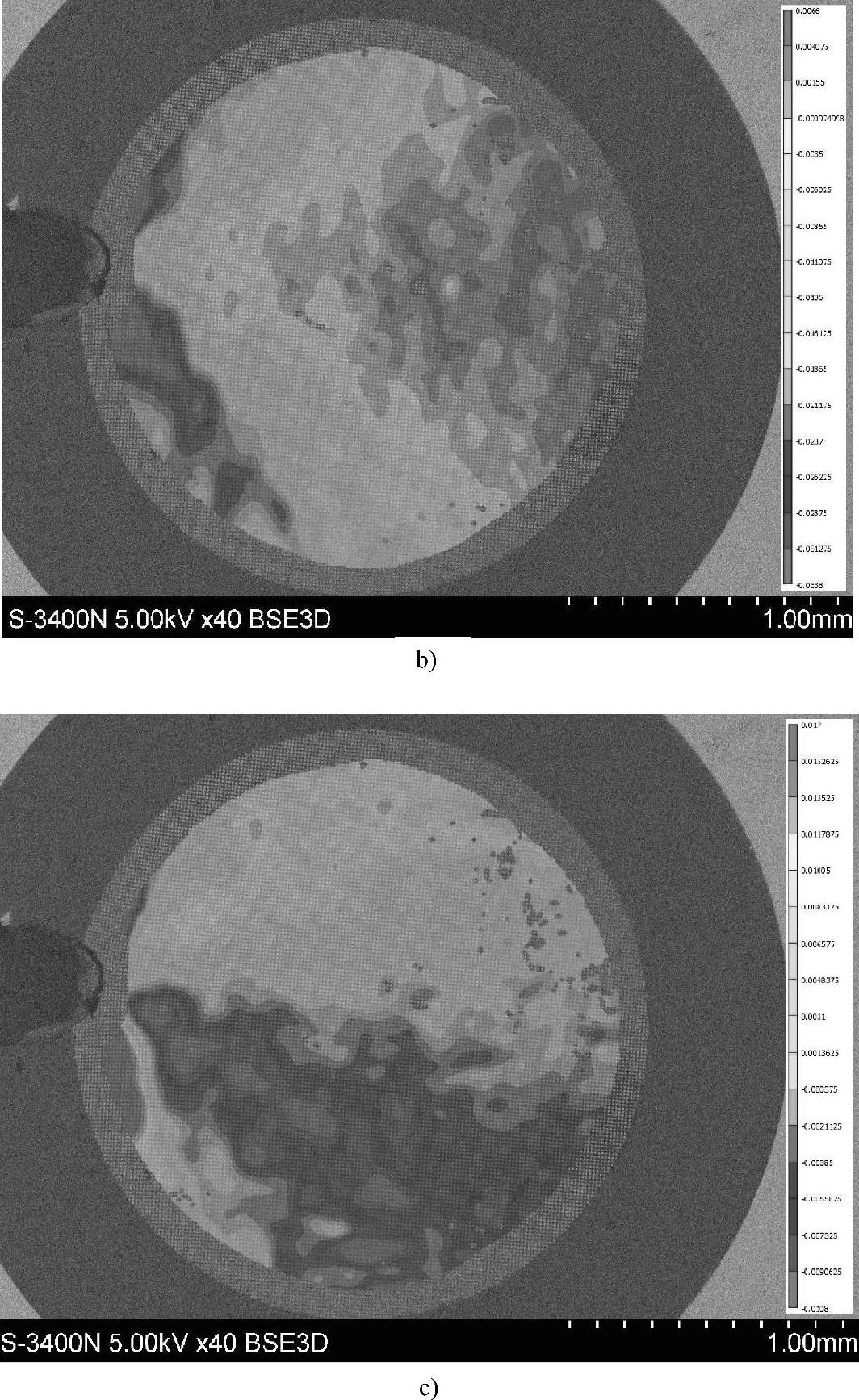
图5-10 用数字图像相关方法测定的裂纹萌生时（对应于图5-4d）裂纹尖端附近的平面应变场（彩图见文后插页）（续）

b）ε_xx应变场 c）ε_xy应变场