实验设计与R语言应用：其他分析方法概述

在上述分析过程中，利用rsm（）函数可以一步得到结果。在实际分析过程中，可以通过等高线法、响应曲面图、最速上升法（岭脊分析法）和线性规划求解方程法从不同侧面理解响应曲面实验数据分析过程，分别介绍如下。

1.图形分析确定最优方案

利用rsm包中contour.lm（）函数绘制等高线图，persp.lm（）函数绘制曲面图，参数at=xs（）表示一并给出最佳水平。

图14-4 等高线图形分析

绘制响应曲面图。

图14-5 绘制响应曲面图

也可以将上述图片存储为PDF格式备用。(www.xing528.com)

2.岭脊分析法确定最优方案（最速上升法）

最速上升法是沿着响应有最大增量的方向逐步移动的方法。实验是沿着最速上升的路径进行的，直到观测到的响应不再增加为止，然后拟合一个新的模型，确定一条新的最速上升路径，持续此过程，最后到达最优点的附近区域。rsm包中函数canonical.path（）只能对二阶回归模型进行岭脊分析。实际操作中可先用较宽的步长计算，方便我们找到行岭脊分析的最佳区域，再缩小步长寻找最优解。steepest（）函数可以对一阶模型做线性上升或者对二阶模型做岭脊分析。建议使用函数canonical.path（）分析。

先用较宽的取值范围计算极值所在范围，显示disc在（-2，2）之间能获得最佳实验效果

通过岭脊分析函数确定最优方案。

3.线性规划求解最优方案

对拟合方程进行求极值，找到最优配比。在R里面可以用函数nlminb（）对一个有约束条件的多元方程求极值（最小值）。具体代码如下，结果与图形分析和岭脊分析一致，convergence为0表示收敛完整。

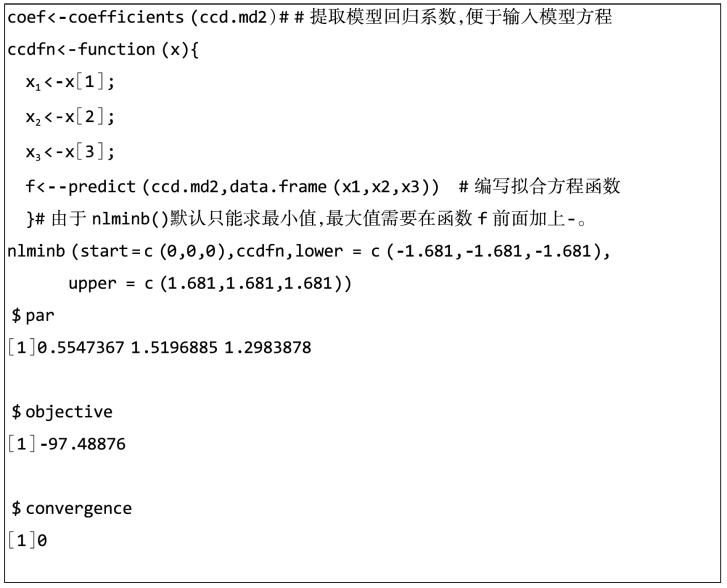
或者使用maxLik包中maxLik（）函数求极值（最大值）。具体代码如下，结果与图形分析和岭脊分析一致。