导入数据只有编码数据的处理方法

导入实验数据，由于这里是直接导入实验结果，表中只有（-1，0，1）编码数据，可以对设计进行重编码，方便后续实验操作和分析。请注意编码方式为x～（因素-中心点）/（因素高水平-中心点）。

先进行一阶线线性拟合，结果显示一阶方程拟合中总模型显著性尚可，调整R平方为0.5267，同时失拟（Lack of fit）显著，预示可能存在二阶曲面作用。当然这是“好征兆”，因为响应曲面设计一般具有二阶效应。

对数据进行二阶分析，SO表示全部二阶作用，包括：FO（一阶），TWI（交互项），PQ（二次项）。二阶方程拟合中显示总模型显著性极显著，调整R平方上升为0.998，同时失拟（Lack of fit）不显著，说明模型可用。同时二阶方程模型给出了因素在曲面驻点位置（Stationary point in original units）料液比、温度、时间（编码水平：0.5547365、1.5196881、1.3528069，实际水平：13.33137、88.96616、27.66049），因素的特征根分析（Eigenanalysis）值均为负，说明上述位置点为最高点。如果均为正说明驻点为最小值，如果特征根同时存在正负说明驻点为鞍点。此时最佳提取回收率为97.48876。

预测顶点的回收率。

通过上述分析我们得到拟合公式如下。(www.xing528.com)

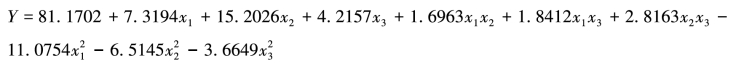
计算回归模型的约束最大值的置信区间（默认为95%）。R包Optima Region可用于计算响应面模型的最佳位置（全局最大值或最小值）上的置信区域。支持参数模型（最多5个协变量中的二次和三次多项式）和非参数模型（2个协变量中的薄板样条模型）。该方法基于bootstrap自举和Tukey数据深度，不依赖于响应的任何分布式假设。通过提供覆盖率分析、证明最佳位置区域的分布和稳定性。

需要注意：最佳提取工艺组合还需要经过实际工作重复验证。这里使用蒙特卡罗模拟（monte carlo simulations）9999次最佳提取条件仿真模拟实验，可以发现回收率可以稳定在97～97.48之间。重抽样：因为观测样本包含了潜在样本全部的信息，那么我们不妨就把这个样本看作“总体”。那么，相关的统计工作（估计或者检验）统计量的分布可以从“总体”中利用蒙特卡罗模拟得到。其做法可以简单地概括为：既然样本是抽出来的，那么何不从样本中再抽样。

图14-3 最佳实验水平模拟抽样图

结论：通过上述分析我们可以获得拟合方程和最佳实验方案。二阶方程拟合显示总模型显著性极显著，调整R平方上升为0.8987，同时失拟不显著，说明模型可用。同时二阶方程模型给出了因素在曲面驻点位置，即：x1为0.555（料液比为13.332），x2为1.52（温度为88.968）和x3为1.298（时间为27.6582）时，提取率能达到最大值97.489。模型方程如上。因素的特征根分析（Eigenanalysis）值均为负，说明上述位置点为最高点。但是仔细观察本实验因素设置还是有可改进的地方（温度和时间的最佳水平离中心点距离较大），可以通过最速上升法更进一步到达最优区域，减少因子水平之间距离，再进行响应曲面设计，优化实验效果。