响应曲面设计,即响应曲面法(Response Surface Methodology,RSM),这是一种实验条件寻优的方法,适宜于解决非线性数据处理的相关问题。它囊括了实验设计、建模、检验模型的合适性、寻求最佳组合条件等众多实验和统计技术;通过对过程的回归拟合和响应曲面、等高线的绘制、可方便地求出相应于各因素水平的响应值。在各因素水平的响应值的基础上,可以找出预测的响应最优值以及相应的实验条件。响应曲面设计将复杂的未知的函数关系在小区域内用简单的一次或二次多项式模型来拟合,计算比较简便,是降低开发成本、优化加工条件、提高产品质量、解决生产过程中的实际问题的一种有效方法。
响应曲面设计的预测模型一般是曲面,即所获得的预测模型是连续的。在实验条件寻优过程中,可以连续的对实验的各个水平进行分析,而正交实验只能对一个个孤立的实验点进行分析。
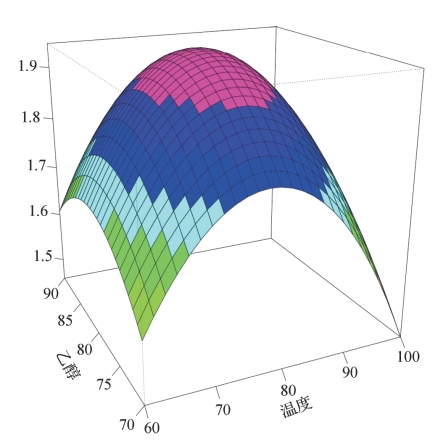
图14-1 响应曲面模型(https://www.xing528.com)
响应曲面优化的前提是设计的实验点应包括最佳的实验条件,如果实验点的选取不当,使用响应面优化法不能得到很好的优化结果的。因此,响应曲面设计主要包含两个阶段。第一阶段:首先判断目前实验区域的状况,它是否已经接近或达到了能使响应变量达到最佳值的最优区域,即是否位于曲面的弯曲“山顶”部分。因此,首先要特别分析数据是否显示了弯曲性,或在数据拟合线性回归方程的方差分析中的“失拟”现象是否显著。如果可以判断弯曲或失拟并不严重,则说明目前实验区域的位置仍然远离最优区域。这时可以用最速上升法(steepest ascent search)寻找实验的最优区域。由于这时的回归方程是线性的,其等高线是近似的平行直线,选取与等高线垂直的方向作为“最速前进方向”(path of steepest ascent),沿此方向继续做实验,直到进入最优区域。第二阶段:选定已得到的最优区域作为新响应曲面设计的中心点,根据实际条件来安排CCD设计或Box-Behnken设计。
响应面分析主要采用的是非线性拟合。最为常用的拟合方法是采用多项式法,简单因素关系可以采用一次多项式,含有交互相作用的可以采用二次多项式,实际应用中三次或更高次数的多项式意义不大。根据得到的拟合方程,可采用绘制出响应面图的方法获得最优值;也可采用方程求解的方法,获得最优值。需要注意的是响应面分析得到的优化结果是一个预测结果,需要实验加以验证。
常见响应曲面实验设计可以通过quality Tools包中的rsm Choose()函数查看。
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




