完全随机实验设计-实验设计与R语言应用

1.完全随机实验的设计

完全随机实验的设计实际上是实验对象随机分组的过程。可以通过随机数或者R中agricolae包的design.crd（）函数实现完全随机实验设计。如需要将18个实验对象完全随机分为5组，每组的实验对象分别是5，4，2，4，3，以下代码可完成完全随机实验设计，并输出实验设计。trt：实验组数，r：每组重复数，serie：标签编号方式，seed：随机种子，kinds：随机方法，有多种随机方法，这里选择default与本书其他章节保持一致。

表11-1 随机实验设计实例

2.完全随机实验数据的分析

当完全随机实验完成后，如果获得的数据是基于实验指标正态分布的计量数据，可以采取参数检验方法进行分析。如为实验数据为计数资料则采用非参数检验。完全随机实验数据的统计分析根据实验处理数不同，统计分析方法有所差异。两个处理的完全随机设计（非配对设计），无论其处理数是否相同都可以采用t检验法分析。多个处理的数据分析一般先进行方差分析，然后在多组之间进行多重比较，判断组间差异。具体分析方法参考前述t检验和方差分析相关章节。这里以单因素多水平为例进行介绍。

现对统计学中某一章的教学方式进行改革，对3个班级分别进行现场讲授式、讨论式、微课式三种教学，教学完成后进行统一考试，成绩如下，请问三种方式对教学效果的影响。导入数据

数据检查、评估检验假设条件（正态性，方差齐性、独立性）

通过summary（）检查数据缺失值，可以看出没有缺失值（显示为NA），使用car包相关函数能够进行异常值分析、正态性检验、方差齐性检验和独立性检验。具体代码请参考方差分析和一元线性回归分析相关章节。这里直接给出检验图示结果，结果表明数据检查符合各项方差分析假设条件，第10行数据可能为强影响点，但库克距离小于0.2，可暂时不处理。

图11-1 模型假设检验汇总图

3.方差分析

利用aov（）函数进行方差分析，需要注意R默认调用类型1方法，与SPSS（类型3）不同，但在本例中只对单因素（class）分析，计算结果没有差别。(www.xing528.com)

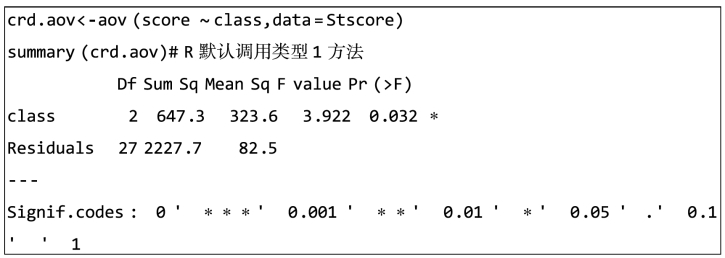
或者使用ezANOVA（）函数完成分析，其中方差齐性检验Levene's for Homogeneity p值大于0.01即可，表明方差齐性满足。type=3表示与其他统计软件调用同样方差类型。比如SAS或SPSS默认调用类型3方法。

4.事后检验

计算各组均值和标准差。

5.可视化结果

绘制箱线图，标记比较结果。

图11-3 使用R内置函数boxplot（）绘制箱线图

6.结论

对3个班级进行教学方法改革。对3个班级各10名同学课后成绩进行分析。测试数据无缺失和异常值，数据满足正态性、方差齐性和独立性检验。使用单因素方差分析，发现教学方式对学生课后成绩有显著影响F（2，27）=3.922，p=0.032。使用LSD法对不同教学方法进行成绩均值比较，讨论式教学班级（M=69.5，SD=7.14）学生平均成绩最高，与讲授式和微课式教学具有显著差异（p=0.04）。微课式教学班级（M=58.5，SD=9.71）学生平均成绩最低，讲授式教学班级（M=60.8，SD=10.10）学生成绩居中，但微课式和讲授式两种方法没有显著差异。