实验设计与R语言应用：方差分析及其概述

前一章介绍的t检验和μ检验适用于两个样本均数的比较。对于k个样本均数的比较，如果仍然采用t检验和μ检验则会显著增加比较次数，同时积累犯第一类错误的概率。因而t检验和μ检验不适用于多个样本均数的比较。方差分析（Analysis of Variance，简称ANOVA），又称“变异数分析”，是R.A.Fisher发明的，用于两个及两个以上样本均数差别的显著性检验，可以有效控制第一类错误。方差分析的检验统计量为F，故又称为F检验。

在实验研究过程中，由于各种因素的影响，研究数据呈现波动。造成波动的原因可分为两类：一类是不可控的随机因素，另一类是研究中所施加的可控因素。因此需要对实验数据进行方差分析以确定是否是研究中所施加的处理因素造成实验数据波动，并找到波动原因。方差分析的主要原理如下：

●实验条件：即不同的处理造成的差异，称为组间差异。用变量在各组的均值与总均值之偏差平方和的总和表示，记作SSb，组间自由度。

●随机误差：如测量误差造成的差异或个体间的差异，称为组内差异，用变量在各组的均值与该组内变量值之偏差平方和的总和表示，记作SSw，组内自由度dfw。总偏差平方和SSt=SSb+SSw。

●F统计量：组内SSw、组间SSb除以各自的自由度（组内dfw=n-m，组间dfb=m-1，其中n为样本总数，m为组数），得到其均方MSw和MSb，F=MSb/MSw

●如果F=1表示组间均值的差异与组内均值的差异近似相等，说明实验处理组间均值没有差异（实验条件处理无效）。如果F≫1表示处理组间均值的变化远远超过处理组内均值的变化，组间的影响因素远超过了组内的随机因素，说明实验处理组间均值有显著差异（不同实验条件处理有效）。(www.xing528.com)

●方差分析：数据必须满足3个条件，即独立、正态，方差齐性。

在R中使用aov（）函数进行方差分析，其主要用法如表7-1所示。

表7-1 常见方差分析的种类及表达式

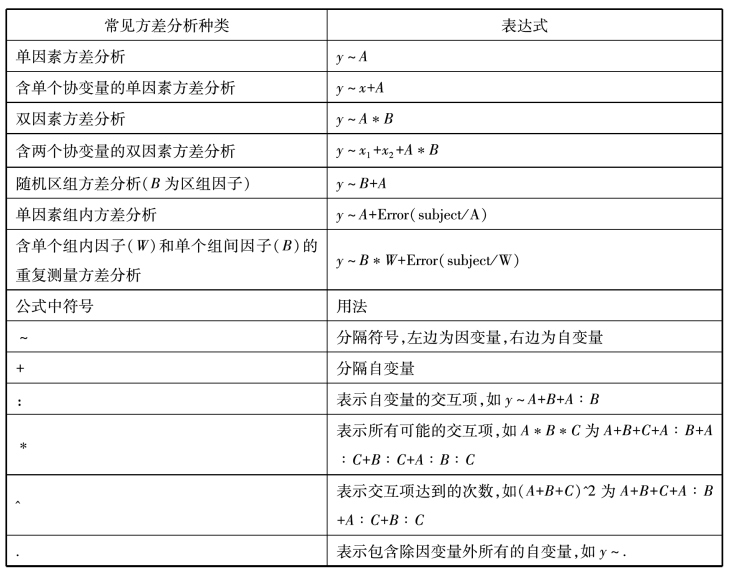
表达式中各项的顺序：当因子不止一个，并且是非平衡设计；存在协变量两者之一时，等式右边的变量都与其他变量相关。此时，我们无法清晰地划分它们对因变量的影响。例如，对于双因素方差分析，若不同处理方式中的观测数不同，那么模型y～A*B与模型y～B*A的结果不同。R默认类型Ⅰ（序贯型）方法计算ANOVA效应，其他软件如SPSS默认采用类型Ⅲ计算（类型Ⅱ和Ⅲ分别为分层和边界型）。R中的ANOVA表的结果将评价：A对y的影响，控制A时，B对y的影响；控制A和B的主效应时，A与B的交互影响。一般来说，越基础性的效应需要放在表达式前面。car包的Anova（）函数提供了三种类型方法，若想与其他软件（如SAS，SPSS）提供的结果保持一致，可以使用它，细节可参考helo（Anova，package=“car”）。