支持向量机的个性化推荐研究：ALTSVM算法描述

给定训练样本集和核函数K，版本空间定义为分类超平面的集合，即在特征空间Hk中可以将训练样本划分开来的所有样本的集合。一般来说，版本空间可定义为：

V={f∈HK|∀i∈{1，2，…，l+u}，yif(xi)＞0。

TSVM利用主动学习选择无标签样本进行标注的原则是选择那些导致版本空间减小最大的样本。

由于式(6.20)等价于，所以存在这样的性质，如性质6.1所述：

性质6.1设l+u个样本确定的版本为：

V={f∈HK|∀i∈{1，2，…，l+u}，yif(xi)＞0}。

当标记了样本(xl+1，yl+1)和(xl+2，yl+2)后，可以得到两个新的版本空间和。如果yl+1f(xl+1)＞yl+2f(xl+2)，那么，则有，其中Area(V)用来表示版本空间的大小。

证明：标记完样本(xl+1，yl+1)和(xl+2，yl+2)后，得到了新的版本空间和。根据决策函数f(x)的表达式，得到新的版本空间，可以表达为：

版本空间：

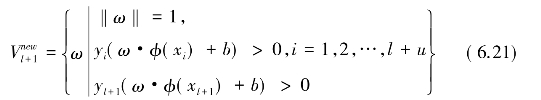(www.xing528.com)

版本空间：

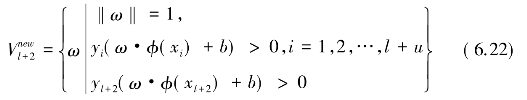
如果yl+1f(xl+1)＞yl+2f(xl+2)，则yl+2(ω·φ(xl+2)+b)＞0。

进一步可得：yl+1(ω·φ(xl+1)+b)＞0。综上可以得：。

从而可以得到结论：。证毕。

从性质6.1可以发现，样本(xi，yi)对应的值yif(xi)越小，标记该样本对应的超平面对版本空间划分后剩余的比例也就越小，从而该样本对训练模型将相当有价值。

基于主动学习的半监督直推式支持向量机的算法描述见表6.1。

表6.1　ALTSVM算法描述
Table 6.1　The description of ALTSVM algorithm