基于支持向量机的个性化推荐方法

在本章提出的基于平滑技术的方法中，用2-范数的松弛变量y并带有权重c1/2，来代替带有权重c1的1-范数y被最小化，见式(5.1)。

采用Lee在文献［156］中提出的方法，松弛变量y可用下面的式子给出：

其中，根据(·)+的定义，用“0”来代替向量中的负元素。从而将y带入式(5.15)，将式(5.15)转化为等价的无约束优化问题，如下：

显然，这是一个不带任何约束的强凸最小化问题。所以该问题具有唯一解。但在(5.17)中的目标函数不是二次可微的。为采用快速牛顿法，采用平滑技术来处理目标函数，使得其可微；并借鉴文献［157］中的方法，用一个非常精确的平滑近似函数来代替(x)+。即采用平滑函数p(x，α)来代替(x)+。比较常见的平滑函数是神经网络中的sigmoid积分函数(1+ε-αx)-1，对于特定的α＞0。平滑函数的表达式如下：

从而，将(5.17)改写为：

其中，α是平滑参数；p(x，α)是平滑函数用来近似加号函数(x)+。本章选择神经网络平滑函数是因为它已经得到了成功的应用［156］。

可以清晰看出，问题(5.17)的解可以通过求解问题(5.19)的同时，使得平滑参数α趋向于无穷大。

首先，证明加号函数(x)+和平滑近似函数p(x，α)之间平方差的上界。

引理5.1对于x∈R和-r＜x＜r，则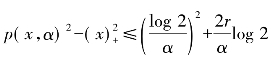，其中，函数p(x，α)是(5.8)中的函数，并且α＞0。

证明：

情况1：当-r＜x≤0时，p(x，α)2是一个单调递增的函数，从而可得：

情况2：当0＜x≤r时，

综上可得：。

从而可以发现：。证毕。

其次，当α趋向于无穷大时，(5.19)的唯一解也趋向于(5.17)的唯一解。

定理5.1设和。定义一个实数值函数f(x)包括(5.17)中的等价函数，并且g(x，α)在n维实数空间中，包括了(5.19)的STWSVM1函数：

和(www.xing528.com)

并且，α＞0。

第一，存在的唯一解和的唯一解。

第二，对于所有α＞0，则存在下面的不等式：

其中，ξ定义为：

从而，当α趋向于无穷大时，趋近于，并且上界为(5.22)给出的上界。

证明：

情况1：证明唯一解存在。我们知道，对于α＞0，p(x，α)≥(x)+以及水平集函数Lv(g(x，α))和Lv(f(x))满足：

所以，Lv(g(x，α))和Lv(f(x))是Rn中的紧致子集，并且和有解。又因为f(x)和g(x，α)是强凸的，所以它们的解具有唯一性。

情况2：为了确认收敛性，注意到一阶最优化条件以及f(x)和g(x，α)是强凸的，从而有：

因为对于所有的α＞0，p函数与(x)+函数满足g(x，α)-f(x)≥0，并结合上面两个不等式，可得：

进一步，应用引理5.1，可得：

如上所述，对于TWSVM2，对(5.23)改写后，得到(5.24)：

类似的，当平滑参数α趋向于无穷大时，(5.24)的唯一解也趋向于(5.23)的唯一解。充分利用QPPs(5.19)和(5.24)的二次可微，可以采用快速的牛顿法来求解它们，该算法已被证明是二次收敛并带有Armijo步长［156］。

为了求解非线性分类问题，引入核函数来构建非线性分类超平面。两个非线性的TWSVMs(5.10)和(5.11)经过平滑函数处理后，得到对应的改写形式：

上述问题能够产生高度非线性分类超平面，并保持强凸性和可微性。所以，定理5.1对(5.25)和(5.26)也成立。同时，也可以采用相同的方法来求解无约束的最优化问题(5.25)和(5.26)。

然而，通过分析式(5.25)和式(5.26)可以发现，在求解它们的时候，存在两个困难。一方面，问题(5.25)具有m2+1个变量，当数据集很大时，m2的阶有可能达到百万级别；并且问题(5.26)中也存在类似的情况。另一方面，所产生的非线性分类平面(5.25)是在整个数据集上(用C表示)得到，这对于大型数据集来说，将会造成存储困难，使得使用非线性核来解决这样的问题越来越不切实际；并且对于(5.26)也存在类似的情况。为了避免这两个困难，采用类似文献［165］的思想，并将注意力转向核减少的平滑对称支持向量机(Reduced Smooth TWSVM，RSTWSVM)。