个性化推荐研究：基于优化支持向量机

在实验中，经典的基准测试函数被设置为粒子的“适应度函数”。为降低偶然因素，每个基准函数被测试10次，并计算其平均值。算法参数的设置为：wstart=0.9；c1，c2=1.5；Tlimit=145；A=0.6；B=0.05。终止条件是适应度函数值达到收敛条件或达到最大迭代次数。

对于所有函数，表4.1表明了IPSO算法优化结果要显著优于标准的PSO算法，并且平均迭代时间明显得到了降低，即IPSO算法可以明显提高粒子的收敛速度。通过观察，对于单峰函数，标准的PSO算法可以得到理论最优值，但是从总体来看，算法的鲁棒性较差。

表4.1　在3个基准函数上对比IPSO算法和PSO算法的性能
Table 4.1　Comparison of IPSO and PSO on the three classic benchmark functions

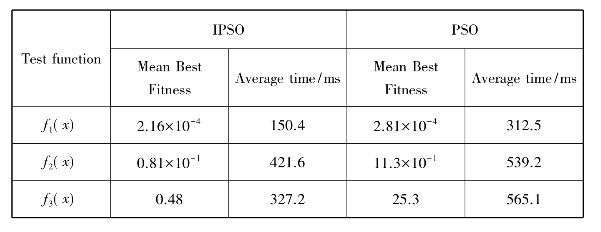
图4.2—图4.4的进化曲线也说明了上述的实验结果。对于图4.2，为了更好地对比IPSO算法和PSO算法，横坐标采用log度量，并且最大的迭代次数设置为300。从这些图中可以发现当求解函数f1(x)时，两种算法之间的性能差别不是很大，并且两种算法都可以收敛到全局最优值，但是IPSO算法的收敛速度比PSO算法要快，需要更少的迭代次数，具有更高的效率；当求解函数f2(x)时，两种算法都可以收敛到全局最优值，但是IPSO算法比PSO算法在收敛速度上具有明显的优势；对于求解函数f3(x)，PSO算法陷入了局部最优解，并且非常难以找到全局最优解。但是IPSO算法可以在很短的时间内收敛到全局最优值，具有很强的优化能力。总言之，在3个基准函数上，IPSO算法要优于PSO算法，为SVM参数优化提供了依据和参考。

图4.2　函数f1(x)的进化曲线
Fig.4.2　The evolution curve of function f1(x)(www.xing528.com)

图4.3　函数f2(x)的进化曲线
Fig.4.3　The evolution curve of function f2(x)

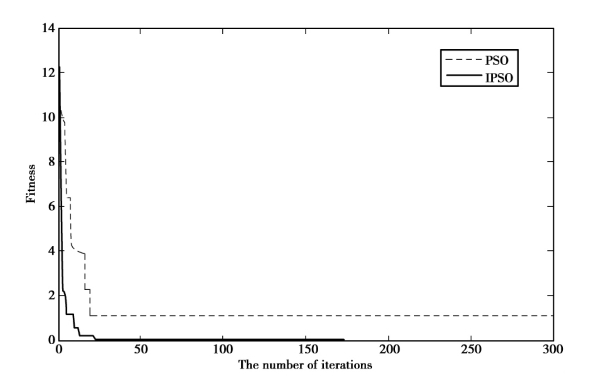
图4.4　函数f3(x)的进化曲线
Fig.4.4　The evolution curve of function f3(x)

由于函数f3(x)的独特性，因此进一步分析函数f3(x)的解。PSO算法非常容易陷入局部最优值，导致算法的收敛速度慢，甚至出现停滞现象。从图4.4可以发现，当进化代数大约等于25时，PSO算法陷入了局部最优值，且出现了停滞现象。然而，IPSO算法跳出了局部最优解，并且很快收敛到全局最优解。因为采用进化速度因子和聚集度因子后，w将能根据粒子迭代的实际情况自适应地调整，进而提高算法的收敛速度和搜索能力。此外，为了防止算法在迭代过程中陷入局部最优值，采用“位置-极值”策略，使算法在陷入局部最优值时，跳出局部最优值。所以，进化速度因子、聚集度因子和“位置-极值”策略可以有效提升PSO算法的性能。