该实验的主要目的是通过UCI数据集测试提出的带收缩因子的动态惯性权重自适应粒子群优化算法CF-IWA PSO的性能,并将该方法与标准粒子群优化算法、遗传算法(Genetic Algorithms,GA)、网格搜索算法(Grid Search,GS)进行对比分析。对于PSO算法和CF-IWA PSO算法的参数设置如下:c1,c2=1.5;wstart=0.9;wend=0.4;粒子的初始速度范围是[-5,5];种群数设置为20;最大迭代次数为100。在SVM预测模型建立时,采用高斯核函数,对应的参数设置为:c的范围设置为[0,100];σ的搜索范围设置为[2-10,210];ε不敏感损失因子的搜索范围设置为[2-10,10],并且在预测模型建立时,采用5折交叉验证。
表3.3给出了5个UCI数据集在CF-IWA PSO算法、PSO算法、GA算法和GS算法下得到的最优参数组合和5折交叉验证下的分类准确率。
表3.3 4种优化算法在UCI数据集上的准确率对比
Table 3.3 The accuracy comparison of four optimization algorithms on UCI
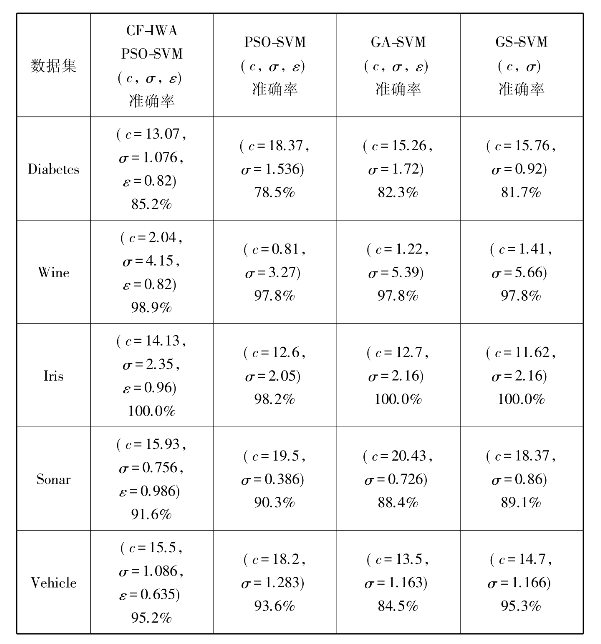
通过表3.3可以发现,本章提出的CF-IWA PSO算法在提升分类准确率方面起到了积极作用。与PSO算法相比,CF-IWA PSO算法在分类准确率上提升较多,并且在每个数据集上,CF-IWA PSO算法都比PSO算法得到的分类准确率高。特别是对于Diabetes数据集,CF-IWA PSO算法比PSO算法得到的分类准确率要更高,可能是因为PSO算法在后期迭代过程中,出现了过早收敛,而没有搜索到全局最优解,陷入了局部最优解。对于GS算法,CF-IWA PSO算法与它的分类性能在很多情况下相当,但GS算法实际上是一种穷举法,常被用在较小范围内搜索最佳的参数组合,并且算法的搜索精度与设置的步长有关。当设置较小的步长时,算法将非常耗时;相反算法的搜索精度将降低,可能不能满足实际的需求。对于GA算法,该算法在实现过程中比较复杂,并且存在早熟现象,容易陷入局部最优值;而CF-IWA PSO算法可以较好的克服局部最优值。
为了进一步验证CF-IWA PSO算法相对于PSO算法存在的优势,将两种算法在迭代过程中的收敛情况和适应度变化情况进行对比分析。图3.5和图3.6分别给出了两种算法在Wine数据集上的适应度(分类准确率)曲线。(https://www.xing528.com)
通过图3.5和图3.6可以发现,CF-IWA PSO算法方法比PSO算法的寻优能力更强,找到的最优参数组合比PSO算法的分类准确率更高。两个适应度变化曲线反映了CF-IWA PSO算法在迭代过程中调整了参数搜索方式,因为采用改进的自适应惯性权重调整策略可以使算法具有更好的适应性,会根据具体的迭代情况,对搜索策略进行相应的改变,以提高算法的搜索能力,防止算法陷入局部最优。对于CF-IWA PSO算法,迭代到第20次后,对搜索策略进行了调整,使算法在迭代过程中搜索到了比PSO更优的参数组合,说明提出的方法具有一定的实用性和有效性。
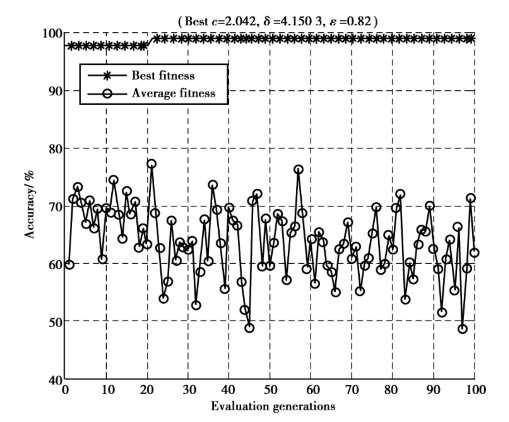
图3.5 Wine数据集在CF-IWA PSO算法下对应的准确率曲线
Fig.3.5 The accuracy of CF-IWA PSO algorithm on Wine dataset
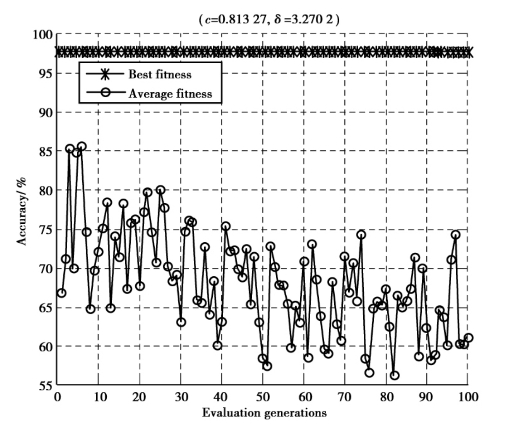
图3.6 Wine数据集在PSO算法下对应的准确率曲线
Fig.3.6 The accuracy of PSO algorithm on Wine dataset
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




