支持向量机个性化推荐研究成果

支持向量机(Support Vector Classifier Machine，SVM)主要分为：线性分类和非线性分类两种情况。对于线性可分，用图3.2来解释。图3.2中的五边形和正方形对应的是正类和负类两种类别(本书用“-1”表示负类，用“+1”表示正类)；H表示分类超平面(hyper-plane)，H1和H2都平行于分类超平面，并称分别通过各分类边界且距离分类超平面最近的样本之间的距离为“分类间隔”。通过观察图3.2，可以发现将两类数据进行正确划分的分类超平面有很多，那么就需要得到这样的超平面可以将两类样本正确划分，训练误差为零，并且使得分类间隔最大，则称这样的超平面为“最优分类超平面”，也就是最大化1/2‖ω‖。

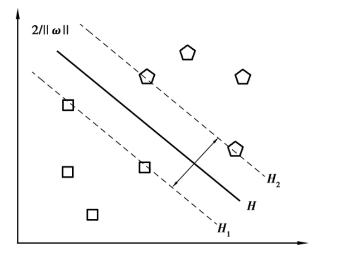
图3.2　支持向量机最优超平面
Fig.3.2　The optimal separating hyper-plane of SVM

对于样本集{(xi，yi)}，其中，xi∈Rn，yi∈{+1，-1}，i=1，…，l。若存在ω∈Rn，b∈R和正数ε，使得对于所有的下标i，当yi=+1时，(ω·xi)+b≥ε；当yi=-1时，(ω·xi)+b≤-ε。进而可以得到统一的表达式yi(ωi·x+b)≥1，i=1，…，l，此时分类器的间隔就为2/‖ω‖，最小化‖ω‖2等价于最大化间隔。进而可知，使1/2‖ω‖2最小化并且满足ω·x+b=0的分类超平面就是“最优分类超平面”，即图3.2中的最优分类超平面。与之对应的位于超平面H1和H2上的训练样本点称为“支持向量”。

为推导出最小化问题的对偶问题，引入拉格朗日函数，得到下面的表达式：

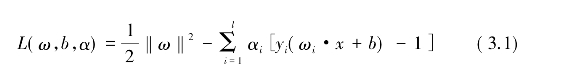
其中，α=(α1，…，αl)是拉格朗日乘子向量。对式(3.1)两边的ω和b分别求偏导数，并令和等于零，从而可得：

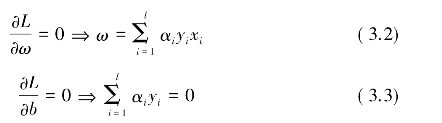
并将其带回L中，可得：

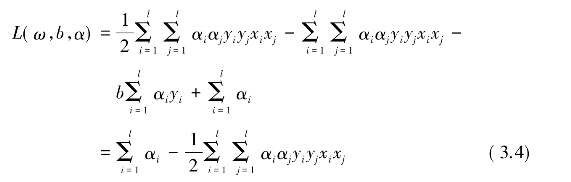
此时，可以得到关于对偶变量α的优化问题：

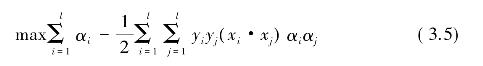
约束条件为：

式(3.5)和式(3.6)为凸二次规划问题，并且存在唯一解。如果该凸二次规划问题的最优解为，则有：

其中，对应的是“支持向量”，从而可得到决策函数为：

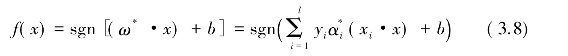
通过式(3.8)可以发现，对于新来的预测样本点x，只需计算它与训练数据的内积即可［其中(xi·x)表示向量的内积运算］。这对支持向量机非常重要，其原因是它采用核函数(Kernel Function)推广到非线性分类的前提基础。进一步观察，“支持向量”也可以在这里显现出来。实际上，对于所有的非支持向量来讲，其对应的系数α都为零。所以，对于新来的样本数据计算内积时，实际上只需要针对少量的“支持向量”，而不是对所有的训练样本数据。经过上面的分析可以发现，支持向量机在分类时，起到关键作用的只有少数的样本，即“支持向量”，其他的训练样本成为了“后方样本点”，对分类超平面没有影响，因为分类完全是由分类超平面决定，所以这些后方的点并不参与分类问题的计算，也就不对分类产生任何影响。

上面介绍的是数据中不存在噪声的情况。而噪声的存在可能对支持向量机的影响很大，毕竟超平面本身是由少数的几个“支持向量”决定，如果在这些“支持向量”中存在噪声，那么其影响就更大。在图3.3中，黑色圆圈圈起来的蓝色样本数据点就是一个噪声点，它偏离了应该所在的分类区域，导致了分类超平面被挤歪，也就是变成了图中黑色的虚线，此时，分类间隔也相应变小。更为极端的情况，将该离群点移的更靠右上角，那么将导致根本无法构造分类超平面。

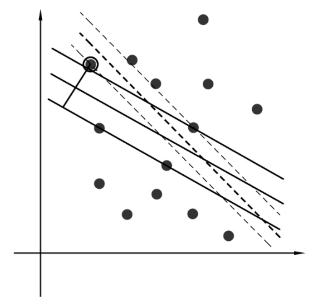
图3.3　噪声数据对支持向量机的影响
Fig.3.3　The effects of noise data on SVM

为了能够很好地处理这种情况，在支持向量机中引入松弛变量，就可以允许数据点在一定程度上偏离分类超平面。例如，图3.3中，黑色实线对应的距离就是该离群点的偏离距离，如果把它移动回来，就恰好落在原来的分类超平面上，而不会引起分类超平面发生变形。也就是说，为解决两类样本点不能被分类超平面完全划分的情况，且希望在推广能力和经验风险之间取得某种平衡，则可以引入松弛变量ξi，那么此时的分类超平面ω·x+b=0满足：

(www.xing528.com)

为了避免松弛变量ξi取值过大，需要在目标函数1/2‖ω‖2中引入惩罚项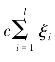，从而式(3.1)转化成了下面的最优化问题：

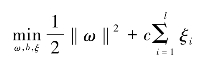
使得　

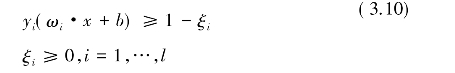
其中，c＞0是惩罚因子，用来控制对错分样本的惩罚程度。

采用前面类似的方法可求得最优分类超平面：

对于非线性分类情况，从理论上讲，可以通过某种非线性变换将其转化为高维空间中的线性可分问题，并在该变换空间中求得最优分类超平面。但在一般情况下，这种非线性变换相当复杂，而支持向量机可以通过核函数变换，巧妙地解决这个问题。

假设存在变换φ：Rn→H，xaφ(x)，使K(x，x′)=φ(x)·φ(x′)，其中，(·)表示向量的内积运算。根据泛函相关理论，如果核函数K(x，x′)满足Mercer条件，那么它就对应某一变换空间中的内积［137］。所以，选择合适的内积函数K(x，x′)就可以实现某一非线性变换后的线性分类，进而避免维度灾难，此时式(3.1)可以转换为：

对应的决策函数为：

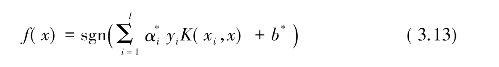
在实际应用中，经常采用的核函数有：

线性核函数(Linear Kernel Function)：

多项式核函数(Polynomial Kernel Function)：

高斯径向核函数(Gauss Kernel Function)：

两层感知核函数(Two Layers Perception Kernel Function)：

关于核函数的选择，要根据实际问题，同时也要对其对应的参数进行合理选择才可以达到理想的效果。