基于图嵌入的高维数据学习方法

Yan等提出了一种基于图嵌入的统一框架，并且PCA、LDA、ISOMAP、LLE和LE在满足一定的约束条件下，都能转换为图嵌入方法。下面首先介绍图嵌入方法及其线性化和核变换扩展，然后具体地分析图嵌入和这些方法之间的变换关系及需要满足的条件。

(1)图嵌入

假设G＝{X，W}是一个无向加权图，其中X是图中的顶点集，W∈Rn×n表示相似度矩阵。矩阵W中的元素表示的是点与点之间的相似度，并且这种相似度可以通过多种方式进行计算。常用的计算模型有热核模型和简单设置模型。在应用热核模型计算相似度时，如果两个点是近邻点，其相似度是通过计算点对之间的高斯函数得到，如果两个点是非近邻点时，其相似度设置为0；当应用简单设置模型时，近邻点之间的相似度设置为1，而非近邻点之间的相似度设置为0。然后通过建立目标函数使得在原始高维空间更相似的数据样本在低维空间也保持相似性。图嵌入方法就是第2章中介绍的LE方法，在这里不再详述。

(2)PCA与图嵌入

PCA能够寻找一个使样本点协方差最大的投影子空间，其目标函数可以表示为:

其中，e＝[1，…，1]T，其他相关矩阵定义如下:

(3)LDA与图嵌入

LDA方法是通过一个线性变换找到具有判别性的子空间。其目标函数是使类间散度的模和类内散度的模的比值最大，即:

对SW和SB推导如下:

因此，当Aij＝δli，lj/nli和D＝H时，它们有相同的目标函数。其中当li＝lj时，δli，lj＝1；否则δli，lj＝0。

(4)ISOMAP与图嵌入

ISOMAP是一种能够保持映射前后测地距离不变的流形学习算法。其目标函数可以表示如下:(www.xing528.com)

其中，τ(DG)＝-HSH/2。对于任何i，可以进行如下推导:

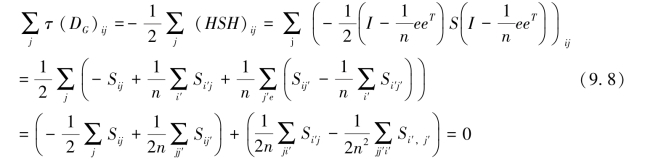
因此，当i≠j时，Aij＝τ(DG)ij；否则Aij＝0，那么目标函数(9.7)可以写成:

(5)LLE与图嵌入

LLE的目标函数为:

进一步转化为:

如果当i≠j时，Aij＝(A＋AT-ATA)ij，否则Aij＝0，则LLE的目标函数可以转化为:

由此可见，PCA、LDA、ISOMAP、LLE、LE及它们的线性化拓展在满足相应约束条件下都可以转换成图嵌入方法。同样，在对这些算法进行核化和张量化拓展后，在满足相应约束条件的情况下，也都可以转换成图嵌入方法。表9-4对这些关系进行了总结。

表9-4　满足不同条件的图嵌入方法与几种常用特征提取方法之间的转换关系

在表9-4算法类型栏中，L表示的是对原算法的线性近似，K表示对原算法的核扩展，T表示对原算法的张量拓展，D表示的是原算法。