高维数据流形学习：目标函数和提纲

根据以上定义的局部统计不相关约束和上一节提出的基于局部线性表示的流形间距准则度量。可以建立目标函数，寻找低维统计不相关子空间，使得流形间距更大。其目标函数如下:

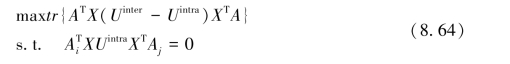
其中，Uinter和Uintra在8.4.3节中已有定义。

另外，为了保证投影子空间的基添加单位化约束，即ATA＝I，目标函数又可以变化为:

寻找一组局部统计不相关A1，…，Ad可以采用如下策略进行。第一个最佳判别向量A1可以通过特征值分解中SMA＝λA第一个最大特征值对应的特征向量组成。假设已经确定前m具有局部统计不相关的单位最佳判别向量A＝[A1，…，Am]，那么第m＋1个局部统计不相关单位最佳判别向量Am＋1就可以由以下约束目标函数进行求解。

对于以上目标函数的求解，首先构造拉格朗日函数:

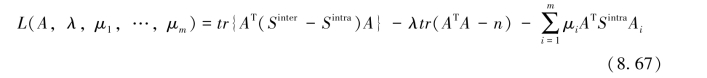
然后，令∂L/∂A＝0，有:

根据上式可以得到:(www.xing528.com)

将上式代入式(8.68)，可以得到:

将式(8.72)代入式(8.71)，得到:

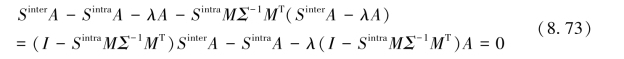
另外，记B＝I-SintraMΣ-1MT，则上式可以改写为:

通过式(8.74)，可以得到如下的特征值分解方程:

因此，在已知前m具有局部统计不相关的单位最佳判别向量A＝[A1，…，Am]，第m＋1个局部统计不相关单位最佳判别向量Am＋1，就是以上广义特征分解中最大特征值所对应的特征向量。

根据以上分析，可以总结CDNE方法的提纲如表8-9所示。