高维数据流形学习分析:CMVM算法模型及提纲

7.3.2.1　多流形相似度度量

欧氏距离也经常用来表示数据点之间的差异。当两个点之间的欧氏距离比较大时，就认为这两点的相似性比较小；相反，当两个点之间的欧氏距离比较小时，就认为这两个点之间的相似性比较大。所以可以采用映射后子流形数据点之间距离的平方和作为衡量多流形间差异的指标。必须指出的是这种差异必须是存在于不同流形之间的，也就是说，计算差异的两个点必须具有不同的类别标签。因此可以建立一个矩阵H来标记任两个数据样本点的类别相似或相异信息。其中H中的元素定义如下:

根据上面类别信息矩阵H，可以定义度多流形之间的相似度JD为:

7.3.2.2　多流形局部几何结构信息度量

在传统的线性特征提取方法中数据点之间的全局几何结构是由数据点之间的欧氏距离矩阵来描述。相应地，输入数据点之间的局部结构也可以用处于近邻关系的数据点对之间的欧氏距离来表示。例如，当两个数据点Xi和Xj是近邻点时，这两个点之间的相似性就可以用下面的欧氏距离计算:

根据数据点之间的近邻关系，定义一个局部关系矩阵L，L中的元素按照以下表达式计算:

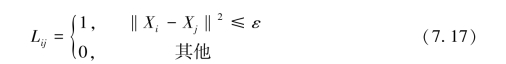
同时L中的元素也可根据高斯函数来定义，其定义为:

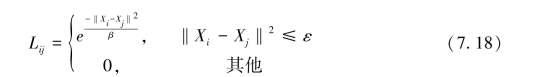
其中，β是调节的参数，ε是阈值。

式(7.17)和式(7.18)中的近邻关系是根据超球标准定义的。另外，k近邻标准也经常被采用。

根据数据点之间的局部关系的定义，可以定义多流形局部几何结构信息度量JL为:

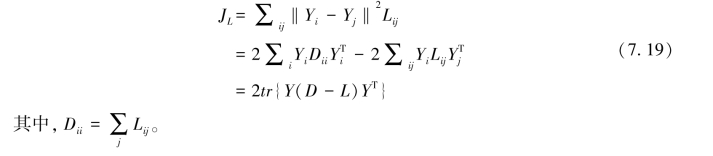
7.3.2.3　线性特征提取

线性特征Y可以通过线性变换得到，即Y＝ATX，其中线性变换矩阵为A＝[A1，A2，…，Ad]。在CMVM算法中，引入线性变换的目的有两点:一是解决样本外点学习能力的问题；二是尽可能地降低泛化学习的计算复杂度。在引入线性变换后，式(7.15)和式(7.19)可分别改写为:

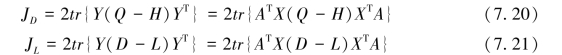
根据前面描述的CMVM算法原理，其约束目标函数可以表示为:

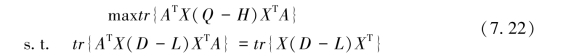
约束目标函数(7.22)的求解可以通过拉格朗日数乘法来实现。首先可以得到一个由目标函数和约束条件组成的线性函数:

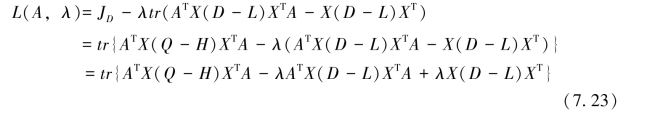
然后对该函数求极值:

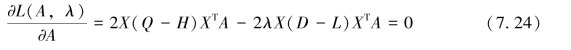(www.xing528.com)

根据式(7.24)可以得到:

从式(7.25)发现，线性变换矩阵A是由以上广义特征方程的广义特征向量所组成。特别地，构成变换矩阵A的广义特征向量对应的是由大到小顺序排列的前d个广义特征值，那么这个线性变换矩阵A将保证目标函数最大。相应的，最佳特征可以通过线性变换Y＝ATX获得。

7.3.2.4　核扩展

CMVM方法采用线性变换来提高算法的泛化能力。另外在核空间，通过核变换也可以提高样本点的泛化学习能力。

其中，Vij是第i个向量Vi的第j个元素，并且Vi是训练样本协方差矩阵的特征向量。

经过核变换之后，原始空间的样本点被映射到一个核空间Φ(X)，在核空间中，JL，JD，H和L都可分别定义为:

因此可将约束优化问题转变为如下的广义特征值分解问题:

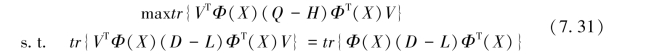
采用拉格朗日数乘法可以得到:

即核变换中向量V是从上式进行广义特征值分解得到，A由d个最大特征值所对应的广义特征向量所组成，并且最后所提取的特征将可以通过式(7.26)进行计算。

7.3.2.5　张量扩展

除了线性化和核化，还可以通过张量化来提高样本点的泛化学习能力。因此，这时的JL，JD，H和L在张量空间可分别定义为:

因此对应的优化问题可改写为:

求解式(7.37)，可以得到其张量映射子空间。

经过以上分析，可以总结线性化CMVM的算法提纲如表7-1。

表7-1　CMVM算法提纲