高维数据流形学习的目标函数及约束条件

在前面的约束条件下，要求处于近邻关系的数据点在投影前后是等距的，并且消除了数据点的平移自由度。在这样的约束条件下，需要怎样一个目标函数才能更好地“伸展”流形数据呢?一般来说，在流形上任意两个数据点之间的折叠都能使这两个数据点之间的欧氏距离变小。也就是说，沿着流形这两个点之间的曲线的曲率越大，它们的欧氏距离就越小。图7-4是欧氏距离与曲率关系图。

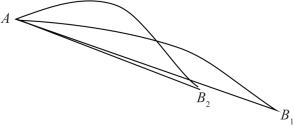
图7-4　欧氏距离与曲率关系图

图7-4中，弧线AB1和弧线AB2的弧长是相等的，分别表示在两个不同流形上的测地距离。弧线AB1的曲率小于弧线AB2的曲率，从图中可以看出，曲率大对应的欧氏距离就小，曲率小对应的欧氏距离就大。欧氏距离与曲率的关系隐含着一种优化准则:如果一个流形展开后的点与点之间的欧氏距离越大，就意味着流形曲面的曲率越小，即这个流形越趋近于平坦，特别是当这些距离和趋近一个极限时，流形在低维空间对应的就是一个超平面，这时投影的效果最理想。所以可以将最大化流形展开后点对之间的距离和作为目标函数。也就是需要找到一个投影变换使得输出点对之间的距离平方和最大，即:

MVU算法是一个约束最优问题。它在满足输出点中心化和近邻点等距离的约束条件下，使得输出点之间的距离或差异最大。在这里，定义一个参数ηij:

其中，Xi∈N(Xj)表示点Xi是点Xj的近邻点。

定义平方距离矩阵D＝(Dij)n×n:

根据上面的定义，该优化问题可以改写成:

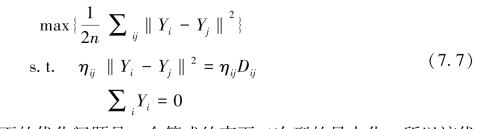(www.xing528.com)

必须注意，因为上面的优化问题是一个等式约束下二次型的最大化，所以该优化问题不是凸优化问题。为了解决这个问题，定义一个内积矩阵Kij＝Yi·Yj，因此式(7.6)可以表示为:

中心化约束也可以改写为:

式(7.8)和式(7.9)是关于Kij的线性约束，此约束条件可视为内积矩阵K的函数。但是，并不是所有的矩阵都能转化成内积矩阵，只有对称半正定矩阵才能进行这样的转换。因此，对这个优化问题必须增加一个约束条件:矩阵K必须是对称半正定的，这个约束条件可以写成K≥0。

通过以上分析我们可以发现，目标函数有三个约束条件:中心化约束、局部等距离约束和对称半正定约束。这三个约束条件都是关于内积矩阵K的约束。目标函数也可以转换成关于内积矩阵K的函数:

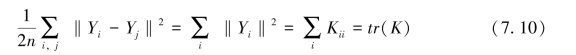
因此整个约束优化问题可以表示为:

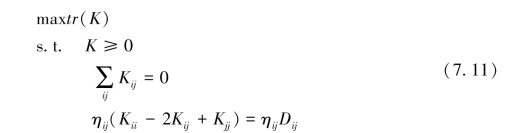
上面的优化问题是一个半正定规划问题:其半正定域是一个锥形被一个超平面所截断形成的封闭区域，且目标函数是内积矩阵K中元素的线性函数。由于满足凸优化条件，所以计算出的最优值不是局部极值。