LLDE算法原理-高维数据流形学习

对于数据的可视化来说，数据维数约简或特征提取的目的是将原始数据点映射到一个二维或三维数据空间，并且尽可能地保存数据点之间的几何拓扑结构。但是对于数据分类而言，数据维数约简或特征提取的目的是将原始数据点投影到具有如下特性的子空间:在该子空间内，不同类别的数据点被映射得很远，而相同类别的数据点被投影得很近。LLE是一种有效的数据可视化方法，这是因为LLE是一种流形学习的方法，它能够使得数据点之间的几何拓扑结构在映射前后近似地保持不变。但是LLE却不是一种很好的面向分类的特征提取方法，这是因为经过原始LLE算法提取的特征体现出很差的分类能力。图6-2是应用LLE算法对一个人工合成数据进行映射的二维可视化结果。从图6-2可以发现，采用LLE方法，将原始高维数据映射到二维投影空间中，三种类别的数据的二维投影相互混杂在一起。

基于原始的LLE算法对数据的分类能力很差的事实，提出一个LLDE模型来改进原始LLE算法的分类效果。LLDE算法的目标是充分利用数据点的类别信息来指导LLE算法的分类。在原始的LLE算法中，最小重构误差对旋转、平移和缩放是不变的。这是因为通过最小重构误差所求得的最小重构稀疏是满足和为1的约束。记Td×n为一个变换矩阵，则通过LLDE后判别分量表示为[Y-T]d×n，得到:

其中，Ti是对于第i类的平移向量。从式(6.1)可以看出最小重构误差对平移具有不变的特点。

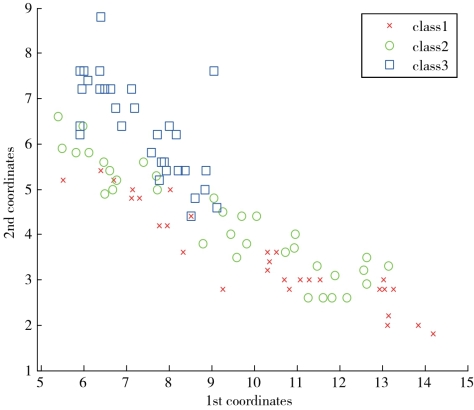
图6-2　经过LLE映射的数据的可视化结果

(www.xing528.com)

图6-3　经过LLE映射进行平移变换的可视化结果

在LLDE方法中，对于具有同一类标签的数据点都平移一个相同的向量，而对于不同类的数据点分别平移到不同的位置。图6-3显示了在LLE映射后对数据进行平移变换的可视化结果。从中可以发现同类的点相对较好地聚集在一起，不同类点之间的质心距离很分散。也就是说经过平移变换后数据点的可分性能大大提高了。对嵌入向量进行平移操作后，我们还可以引入一个缩放因子。在保持每类数据的质心不变的基础上，缩小同类点与质心的距离，从而提高数据的可分性能。图6-4显示了经过平移和缩放变换后数据的可视化结果。从图6-4可以看出数据点的分类能力得到了很大的提高。

图6-4　经过LLE映射的数据进行平移和缩放变换的可视化结果

这些可视化效果图证实了通过平移和缩放变换能够显著地提高数据点的可分能力。从理论上来说，这种方式是可行的。但是从实际应用的角度来看，通过平移和缩放变换，提高数据点的分类能力却是不可行的。因为在实际应用存在着如何选择平移向量和缩放因子才能使数据点的分类能力达到最佳的问题。为了解决这个问题，提出一个改进最大间距标准(Modified Maximizing Margin Criterion，MMMC)来寻找最佳的平移和缩放变换，提高数据的可分能力。同时为了克服原始LLE算法中的样本外点学习能力差的问题，引进一个线性变换，同时也能大大降低算法的计算复杂度。

综上所述，LLDE算法的目的是要找到一个线性变换，使其既能满足LLE算法的最小重构误差的要求，又能满足MMMC的最佳平移和缩放变换的要求。同时，该线性变换不但能够解决原始流形学习算法中存在的样本外点学习能力问题，还可以很大程度地降低算法的计算复杂度。