高维数据流形学习方法解析

5.4.2.1　距离度量

(1)点到特征线(Point to Feature Line，P2L)距离

点到特征线的距离可以定义为点到该点在特征线上的投影之间的欧氏距离，其示意图如图5-8所示。

图5-8　点到特征线距离示意图

其中，sm，n和sn，m是两个加权系数，并且加权系数sm，n可计算如下:

由上式可知:

(2)点到特征平面(Point to Feature Super-Plane，P2SP)距离

点到特征平面的距离定义为点与该点在超平面的投影的距离，其示意图如图5-9所示。

图5-9　点到特征空间距离示意图

点到特征超平面的距离如下式所示:

其中，sq，f可以通过下式计算:

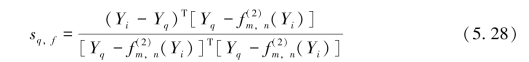
由式(5.27)可知，加权系数sm，sn和sq满足:

(3)点到特征空间(Point to Feature Space，P2S)距离

对于特征平面而言，一般是由三个样本点组成。对于由多于三个的数据点组成的就是特征空间。那么点到特征空间的距离定义为点与该点到特征空间的投影之间的距离:

(4)特征空间到特征空间(Feature Space to Feature Space，S2S)距离

流形学习常常采用k近邻方法来学习样本数据的局部结构信息，同时对于任意一个样本点而言，它的k个近邻点就构成了该样本的特征空间，该样本本身就是特征空间的核心点。上节已经定义了点到特征空间的距离，那么在此基础上可以定义特征空间到特征空间的距离为核心点对在各自特征空间内的投影之间的欧式距离。如图5-10中的粗实线所示。

图5-10　特征空间到特征空间距离示意图(www.xing528.com)

因此，特征空间到特征空间距离可计算如下:

5.4.2.2　异类样本数据点的分离度和同类样本数据点的聚集度度量

(1)异类样本数据点的分离度度量

首先定义异类样本数据点的类别相异度如下:

然后根据异类近邻样本点的类别相似度，建立基于特征空间到特征空间距离的异类图Laplacian谱作为异类样本数据点的可分离度的度量:

(2)同类样本数据点的聚集度度量

对于类别相同的近邻点，首先建立类别相似度度量:

在此基础上，建立能表示同类数据之间聚集度或者是同类样本数据的局部几何结构信息的度量。

5.4.2.3　基于特征空间距离度量学习的判别图嵌入

对于数据分类而言，要求同类数据更聚集，异类数据更分散。因此建立如下目标函数实现高维数据在低维空间的判别投影:

为了解决小样本问题，在原始数据和低维投影之间引入线性变换Y＝ATX，则有:

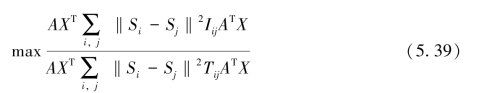
对上式进行展开，有:

其中，Linter是基于特征空间距离的异类近邻图Laplacian谱，Lintra是基于特征空间距离的同类近邻图Laplacian谱。

最后，以上目标函数的求解可以转化为求解广义特征值分解，即线性变化矩阵A如下广义特征分解中前几个最大特征值对应特征向量组成:

根据以上分析，所提出的特征空间距离度量学习的判别图嵌入方法的提纲总结如表5-5所示。

表5-5　FSDML方法提纲