高维数据流形学习分析方法-Box统计分析

4.3.3.1　箱线图Boxplot

Boxplot(即箱线图)是一种常用的统计工具。它以一个简单的组合图形将数据的形状直观地表现出来，使人们能比较直观地发现隐含在数据中的结构信息。箱线图作为一种统计工具，其功能具有独特之处，它能直观明了地识别批数据中的异常值。数据中的异常值是值得关注的，忽视数据中的异常值是十分危险的，这是因为如果不加剔除地把异常值包含到数据的计算分析过程中，会给结果带来不良影响；重视异常值的出现，分析其产生的原因，常常会成为发现问题进而改进决策的契机。箱线图提供了异常值识别的一个标准:异常值被定义为大于{Q3＋1.5(Q3-Q1)}和小于{Q1-1.5(Q3-Q1)}的值，其中Q1和Q3分别是1四分位数和3四分位数。虽然这种标准看起来是任意的，但它来源于经验判断，因为经验表明它在处理需要特别注意的异常值数据效果很好。箱线图方法与识别异常值的经典方法有所不同。众所周知，常用的一些统计方法是以假定数据服从正态分布为前提的，但实际数据往往并不严格服从正态分布。它们判断异常值的标准是以计算批量数据的均值和标准差为基础，但是均值和标准差的耐抗性极小，异常值会对均值和标准差产生较大影响，这样就要求一个数据中包含的异常值个数不能多于数据总数的0.7%。显然，应用这种方法来判断非正态分布数据中的异常值，其效用是有限的。箱线图依靠实际数据来绘制，不需要事先假定数据服从某种特定的分布形式，对数据没有任何限制性要求，它只是真实直观地表现数据形状的本来面貌。另外，箱线图判断异常值的标准以四分位数为基础，四分位数具有一定的耐抗性，多达25%的数据可以变得任意远，却对四分位数不会产生很大的扰动，异常值不能对这个标准施加太大的影响，因此通过箱线图来识别异常值是比较客观的。由此可见，箱线图在识别异常值方面具有一定的优越性。

4.3.3.2　箱线图的参数

箱线图通过四分位数成功地发现数据中的奇异值。四分位数是根据箱线图中的有关参数计算的，箱线图包括五种重要参数，分别列举如下:

①最小值

②1四分位数Q1

③中线，也就是平均值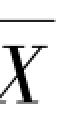

④3四分位数Q3(www.xing528.com)

⑤最大值

根据以上5个参数就可以绘制箱线图，其示意图见图4-5。

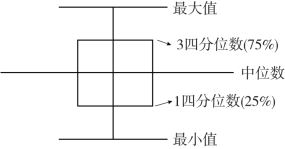
图4-5　Boxplot参数示意图

4.3.3.3　基于Boxplot方法的噪声识别

前面我们通过IRLS算法已经对每一个点(包括噪声点和干净点)进行了赋权处理，得到其对应的权值。这个权值反映了该点是噪声点的可能性。因此可以用箱线图工具分析各数据点的权值来识别噪声。也就是说，如果数据点的权值是奇异值，那么它就是噪声。另外，在定义奇异值的上限{Q3＋1.5(Q3-Q1)}和奇异值的下限{Q1-1.5(Q3-Q1)}时，设置了一个参数α∈[1.0 1.5]，而不是仅仅将其固定在1.5，这样通过调节α的大小就有可能更有效地识别数据中的噪声。因此奇异值的上限可以定义为{Q3＋α(Q3-Q1)}，相应地下限可以定义为{Q3-α(Q3-Q1)}。权值大于{Q3＋α(Q3-Q1)}和小于{Q3-α(Q3-Q1)}的点将被视为噪声点。