高维数据流形学习分析方法及结果

传统流形学习方法包括ISOMAP、LLE和LE，在建模的过程中对采样数据的要求较高，需要数据均匀稠密采样。因为流形学习方法是通过样本数据的局部几何信息学习和保持实现高维数据到低维空间的映射。但是如果训练样本不是均匀稠密的，极端情况是数据存在孔洞，那么在应用ISOMAP、LLE和LE算法去学习这些孔洞边缘数据时，往往会因为缺少必要的数据量，不能充分地学习流形数据的局部几何结构信息，因此造成这些流形学习方法的失败。图3-2显示的是采用ISOMAP和LLE方法对有孔洞的Swiss Roll数据映射的结果。从中可以发现ISOMAP和LLE对有孔洞的Swiss Roll数据是失效的。

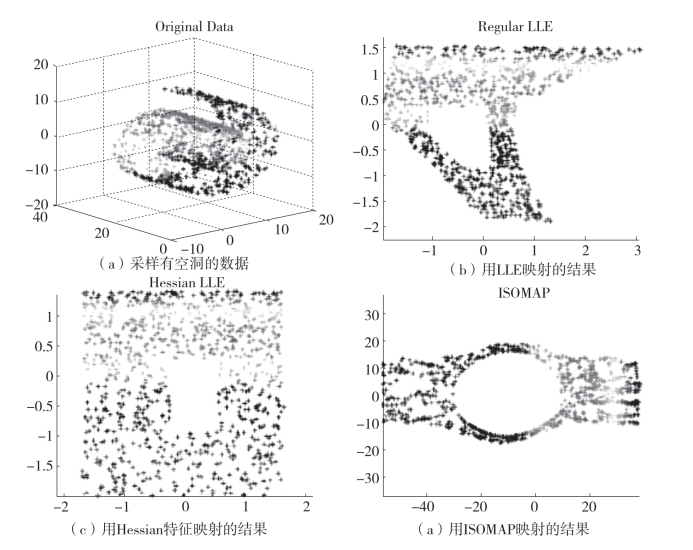
图3-2(www.xing528.com)

为了解决上述问题，有研究者在进行流形局部结构学习建模时，不是从流形局部超平面进行局部几何结构的学习，而是对应于任何一个样本点，建立局部切空间模型，然后在局部切空间内进行各种仿射变换，实现对不均匀稠密分布数据的局部几何信息的充分学习。例如Hessian LLE和Hessian LE就是基于LLE和LE在局部切空间进行局部学习的改进流形学习方法，LTSA也是从局部切空间建模出发，进行不均匀分布特别是有孔洞数据的局部结构学习的流形学习方法。从图3-2中也可以发现，采用Hessian LLE算法对有孔洞的Swiss Roll数据进行投影能够获得比较理想的低维嵌入结果。因此，在流形局部，通过建立局部切空间映射模型，将高维数据投影到一个低维映射空间，就不像ISOMAP、LLE和LE方法，不要求数据集一定是凸的。