高维数据流形学习分析方法

随着信息技术的飞速发展，人们从国民经济各行业所获得的数据正在以指数级的形式快速增长，其中大量不确定性数据和海量模糊数据体现了高维小样本的特点。例如，在计算机视觉、图像分析、网络数据检索、基因微阵列数据分析、生物特征识别以及视频检索中获取的数据都具有高维的特点。目前人们对这些高维数据的处理还没有一种通用有效的方法，在处理这些数据时，传统的数据分析方法往往收效不大，甚至没有效果，蕴含在数据中的信息或规律无法被探索和理解，导致“数据资源”变成“数据灾难”。然而，信息技术的发展又迫切需要去探索和揭示存在于这些数据之间的奥秘。因而，如何有效地从高维数据中获取信息或规律，已经成为当今信息科学与技术所面临的基本问题。将现代计算机的高性能与人的高智能相结合是处理这些数据最有希望的选择，也是处理高维数据最有效、最核心的技术与途径，其中数据挖掘和机器学习已经被证明是行之有效的数据分析和处理方法。在数据挖掘和机器学习的许多应用领域如模式识别和生物信息学，常常需要对这些数据建立一个分类器模型和学习算法，成功探索和挖掘存在于高维数据中一些未知的规律。计算机对高维数据进行处理和识别过程通常包含以下四个方面:

(1)信息获取

通过传感器或其他的信息获取装置采集语音、图像、字符、视频、基因和蛋白质等原始数据。

(2)数据预处理

对上一步获得的原始数据进行一些必要的处理，从中获得需要的数据。例如，原始收集的数据在收集过程中由于气候、温度和人工因素等影响往往伴随着很多噪声，由于这些噪声的干扰，原始数据不能被正确地认识。另外，通过数据获取装置获得的数据也可能包含着一些无用的信息，比如对植物叶片进行识别过程中所获得的叶片图像可能存在于很复杂的背景中，从这些复杂背景中分割出叶片图像或者去掉与叶片识别无关的背景图像也是一个必需的数据预处理过程。

(3)数据的特征提取与选择

在一个比较完善的模式识别系统中，特征提取与选择技术是一个重要环节，处于对象数据采集和分类识别两个环节之间，特征提取与选择方法的优劣极大地影响着分类器的性能，它是模式识别的核心问题之一。特征提取与选择的基本任务是研究如何从众多特征中挖掘出那些对分类识别最有效的特征，从而实现特征空间维数的压缩。数据的特征提取常常是通过维数约减实现的，在满足某种约束条件的基础上，实现目标优化，通过相应的变换将高维数据映射到低维空间中，获得所需要的特征。

(4)分类器设计和分类决策

模式识别的目的就是通过已知数据的相关信息来建立一种分类器模型和分类决策学习算法，并且能够利用这种模型和学习算法，有效地探索存在于数据中的未知规律，实现样本数据的正确分类。

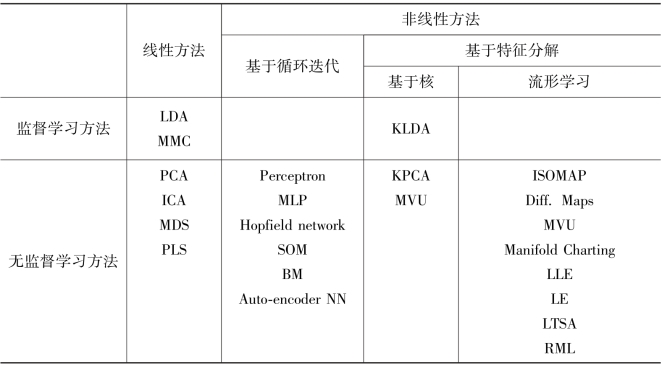
图1-1是数据处理和模式识别的流程图。在模式识别的整个过程中，特征提取或维数约减和分类器设计是模式识别研究的重点。多年来，通过数学、信息学和计算机科学等领域有关专家学者的不懈努力，模式识别研究特别是对数据的特征提取或维数约简研究已经取得很大的进展，提出了很多特征提取方法。依据是否利用了样本的类别信息，这些方法可划分为有监督(或称为外监督)和无监督两种类型的特征抽取方法。近年来，有些特征提取方法中只是部分数据用到样本的类别信息，因此半监督特征提取方法也越来越受到人们的关注。根据特征提取方法的变换方式是否是线性的，这些方法也可以分为线性和非线性的。表1-1是一些常用特征提取方法的分类。

(www.xing528.com)

图1-1　数据模式识别的流程图

长期以来，线性模型的研究一直是机器学习发展的主流方向。基于数据是全局线性分布的假设，传统线性模型中各观测变量是相互独立的，因此欧几里得距离(欧氏距离)常常被用来作为一种相似性度量。以这种假设为基础的众多线性方法，例如线性判别分析(Linear Dicriminant Analysis，LDA)和主成分分析(Principal Component Analysis，PCA)等在很多应用领域都取得了较好的应用效果。

表1-1　常用特征提取方法分类

对于全局线性数据，线性特征提取方法已经被证明是有效的。然而在现实生活和实际应用中，很多数据并不完全是全局线性的。在数据的采样过程中，人们常常发现，现实世界的一些模式往往服从一定形式的非线性分布规律。这些分布规律使数据之间互相影响、互相制约，即使是同一种模式的数据，在不同外界环境作用下，也可能表现出多种形态。例如，同一个人的不同人脸图像可以由，光照、姿态和表情等关键因素决定，这些关键因素中的每一种发生变化时都会引起人脸图像中的像素发生变化，而且这些关键因素同时变化所引起的像素的共同变化，也不是由每一种关键因素变化所引起的像素变化的简单线性叠加，也就是说，光照、姿态和表情条件变化下的人脸数据是高度非线性的。从几何角度来看，这样的人脸图像数据是位于一个嵌入高维空间的低维流形上的。在现实世界中，除了人脸数据，还存在大量的服从低维流形分布的数据，包括手写体数字、植物叶片图像、步态以及手势变化等图像，这些数据常常具有内在低维流形结构。然而，传统线性维数约减方法并不能有效地探索存在于非线性数据中的内在规律。因此，对于大量的非线性分布数据，需要建立非线性学习模型，发展非线性维数约减方法，探索蕴含在数据中的非线性分布规律。

为了研究大量的非线性分布数据，很多研究者提出了许多非线性维数约减方法。这些方法按照其计算方式的不同，可分为基于循环迭代求解和基于特征值分解的方法。其中人工神经网络(Neural Network，NN)方法为非线性数据的处理提供了一种基于循环迭代求解的途径，其代表性的算法是自组织映射方法(Self-Orgonizing Mapping，SOM)。人工神经网络方法的特点是输入信号能够通过神经网络映射到低维空间，在低维空间中仍然保持高维空间数据点之间的近邻关系。另一种通过循环迭代来求解的代表性非线性维数约减方法是主曲线方法(Principal Curves，PC)，该方法本质是线性主成分方法的非线性扩展。近年来，随着深度学习的发展，一批基于深度学习的神经网络模型逐渐建立起来。其中典型深度神经网络模型包括Autoencoder神经网络模型，深度信念网络模型和文本深度表示模型等。但是无论传统的神经网络模型还是基于深度学习的神经网络模型，都是通过不断地循环迭代来求解最优值。这些方法能够比较有效地解决非线性数据的处理需求，但是由于它们毫无例外地采用循环迭代的思想，不可避免地产生下列缺陷:一是使得在循环求优的过程中容易产生局部极值而不是全局极值；二是不断进行的循环迭代容易产生积累误差；三是求解过程需要付出昂贵的计算代价，特别是在训练样本集很大的情况下。

目前，一些基于特征值或广义特征值分解的方法已经被有效地应用到数据处理过程中，其中代表性的方法是核变换方法和流形学习方法。核变换方法通过核变换将具有非线性结构的数据投影到一个核空间，使其线性可分。因此，在原有的线性特征提取方法的基础上，通过核变换就变成一种非线性方法，这也为非线性数据的处理提供了一种有效的途径。代表性方法有核主成分分析(Kernel Pricinpal Component Analysis，KPCA)和核Fisher判别分析(Kernel Fisher Discriminant Analysis，KFDA)。但是由于核变换过程中引进了核函数，在提高算法性能的同时，也在一定程度上升高了样本的维数，而且算法的性能与核函数的选择及参数的设定密切相关。对于不同的数据，如何选择核函数和设定理想的核参数，是迫切需要解决的问题。但是到目前为止，还没有发现一种可遵循的准则，多数情况下核模型和核参数的选取仍然需要经验指导。

流形学习方法是近年来才发展起来的一类新的非线性维数约简方法，也有研究者将前面提到的线性方法、人工神经网络方法、主曲线方法和核变换方法等统称为流形学习方法。在本书中，我们所提到的流形学习方法特指基于局部线性的流形学习方法。流形学习方法的应用对象是嵌入在高维空间的非线性低维流形数据。在认知过程中，人类往往是通过这种非线性低维流形来识别事物的。正如前面所述，高维空间中的人脸图像可以看做分布在以姿态、表情和光照条件为本征特征或自由度的低维流形上的。人们之所以能够很快地识别这些图像，正是因为他们能够识别这些本征特征。流形学习方法能够自动地探测出低维流形的本征维度，这说明应用流形学习方法进行数据处理是合理和可行的。但是，流形分布数据的非线性给流形维数约简方法的建模带来了很大的困难。为了解决这个问题，Tenenbaum和Roweis提出了一种基于局部线性、全局非线性的解决方案，在此基础上构建了两种流形学习算法:等度规映射算法(Isomatric Mapping，ISOMAP)和局部线性嵌入算法(Locally Linear Embedding，LLE)。这两种方法的提出，开创了机器学习领域中流形学习的新流派。随后一批代表性的流形学习算法纷纷涌现出来。Belkin等提出了一种拉普拉斯特征谱方法(Laplacian Eigenmaps，LE)。为了解决数据不均匀采样或者数据样本点存在孔洞的问题，Donoho等提出了海森特征谱方法(Hessian Locally Linear Embedding，HLLE)，Zhang等提出了局部切空间排列算法(Local Tangent Space Alignment，LTSA)。随后，又有研究者提出了半正定嵌入算法(Semi-Definite Embedding，SDE)，并且将该算法发展成为最大差异伸展算法(Maximum Variance Unfolding，MVU)，该算法的一个很大的特点就是引入核矩阵，通过对核矩阵的半正定约束来实现数据的凸优化(Convex Optimization，CO)，因此MVU在一定程度上也可以看做一种基于核变换的学习算法。另外，Lin等成功地提出了基于局部切空间的Riemann流形学习方法(Riemann Manifold Learning，RML)。随着研究的不断深入和推广，流形学习方法也从原来的无监督学习推广到了有监督学习和半监督学习，从非线性化扩展到线性化、张量化和核化，在机器学习领域受到了研究者越来越多的关注和重视。

流形学习方法为探索非线性分布数据的内在流形结构提供了一种可能途径。但是在实际应用中，流形学习方法仍然存在一些缺点，比如对噪声敏感、要求稠密均匀取样和泛化能力差等。为了解决这些问题，相关的算法也在不断涌现。Chang等提出了一种鲁棒局部线性嵌入算法(Robust Locally Linear Embedding，RLLE)来消除原始的局部线性嵌入算法对噪声敏感。海森特征谱方法和局切空间阵列方法的提出解决数据数据不均匀采样甚至存在孔洞的问题。Choi等成功地将Mercer核引入ISOMAP算法中，提高了原算法的泛化学习能力，同时还发现新算法能够有效地抑制噪声的影响。这些方法的提出在一定程度上解决了目前流形学习方法中存在的一些问题，但是还需要进一步充实和完善。